
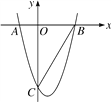
【题目】如图,已知抛物线y=x2-x-6与x轴交于点A和B,点A在点B的左边,与y轴的交点为C.
(1)用配方法求该抛物线的顶点坐标;
(2)求sin∠OCB的值;
(3)若点P(m,m)在该抛物线上,求m的值.
【答案】(1)抛物线的顶点坐标为![]() ;(2) sin∠OCB=
;(2) sin∠OCB=![]() ;(3) m1=1+
;(3) m1=1+![]() ,m2=1-
,m2=1-![]() .
.
【解析】(1)根据配方法,可得顶点式解析式,根据顶点式解析式,可得抛物线的顶点;
(2)根据函数值为0,可得B点坐标,根据自变量为0,可得C点坐标,根据勾股定理,可得BC的长,根据正弦的意义,可得答案;
(3)根据图象上的点的坐标满足函数解析式,可得一元二次方程,根据解一元二次方程,可得答案.
解:(1)∵y=x2x6=x2x+![]()
![]() 6=(x
6=(x![]() )2
)2![]() ,
,
∴抛物线的顶点坐标为(![]() ,
,![]() );
);
(2)令x2x6=0,
解得x1=2,x2=3,
∴点B的坐标为(3,0),
又点C的坐标为(0,6),
∴BC=![]() ,
,
∴sin∠OCB=![]() ;
;
(3)∵点P(m,m)在这个二次函数的图象上,
∴m2m6=m,
即m22m6=0,
解得m1=1+![]() ,m2=1-
,m2=1-![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
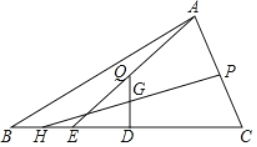
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
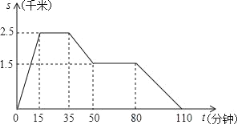
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书,然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离s(千米)与离家的时间t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为多少千米,书店离家的距离为多少千米;王亮同学在书店待了多少分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为( )

A. 20![]() 米 B. (20
米 B. (20![]() -8)米 C. (20
-8)米 C. (20![]() -28)米 D. (20
-28)米 D. (20![]() -20)米
-20)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的变化是人们在生活中经常谈论的话题,请你根据下图回答下列问题:
(1)上午9时的温度是多少?这一天的最高温度是多少?
(2)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
(3)在什么时间范围内温度在下降?图中的A点表示的是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 ;
(2)如图 1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB 为勾股边且有对角线相等的勾股四边形 OAMB 的顶点M 的坐标: ;
(3)如图 2,将△ABC 绕顶点 B 按顺时针方向旋转 60°,得到△DBE,连接 AD、DC,∠DCB=30°.求证: DC2 BC2 AC2 ,即四边形 ABCD 是勾股四边形;
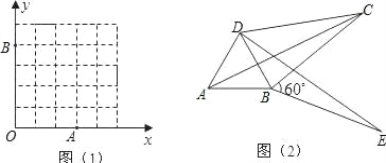
(4)若将图 2 中△ABC 绕顶点 B 按顺时针方向旋转 a 度(0°<a <90°),得到△DBE,连接 AD、DC,则当∠DCB= °时,四边形BECD 是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
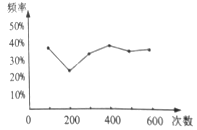
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com