
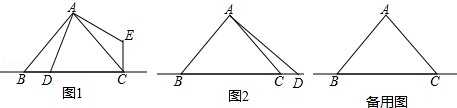
���� ��1���ɵ���ֱ�������ε����ʵõ��������жϳ���BAD�ա�CAE���ɣ�
��2��ͬ��1������һ����
��3�����ݹ��ɶ������㼴�ɣ�
��� ��1��֤������ͼ1��
�ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
�ߡ�DAE=90�㣬
���DAE=��CAE+��DAC=90�㣬
�ߡ�BAC=��BAD+��DAC=90�㣬
���BAD=��CAE��
�ڡ�BAD�͡�CAE�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAE}\\{AD=AE}\end{array}\right.$
���BAD�ա�CAE��SAS����
��BD=CE����ACE=��ABC=45�㣮
���BCE=��ACB+��ACE=90�㣬
��BD��CE��
��2����ͼ2��
���߶�AD�Ƶ�A��ʱ�뷽����ת90��õ��߶�AE������CE��
�루1��ͬ����֤CE=BD��CE��BD��
��3��2AD2=BD2+CD2��
�ߡ�EAD=90��AE=AD��
��ED=$\sqrt{2}$AD
��RT��ECD��ED2=CE2+CD2��
��2AD2=BD2+CD2
���� �����Ǽ��α任�ۺ��⣬��Ҫ��������ת�͵���ֱ�������ε����ʣ��жϳ���BAD�ա�CAE�ǽⱾ��Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
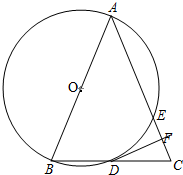 ��ͼ��ABΪ��O��ֱ������DΪ��O�ϵ�һ�㣬��BD���ӳ�����ȡ��C��ʹDC=BD��AC���O���ڵ�E��DF��AC�ڵ�F����֤��
��ͼ��ABΪ��O��ֱ������DΪ��O�ϵ�һ�㣬��BD���ӳ�����ȡ��C��ʹDC=BD��AC���O���ڵ�E��DF��AC�ڵ�F����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬλ����� | B�� | ȫ�������εĶ�Ӧ����� | ||
| C�� | ��a=b����|a|=|b| | D�� | ���������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
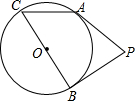 ��ͼ����P�ڡ�O�⣬PA��PB�ǡ�O�����ߣ�A��B���е㣬BC��ֱ��������APB=70�㣬���ACB�Ķ���Ϊ55�㣮
��ͼ����P�ڡ�O�⣬PA��PB�ǡ�O�����ߣ�A��B���е㣬BC��ֱ��������APB=70�㣬���ACB�Ķ���Ϊ55�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com