
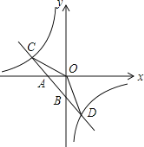
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
【答案】(1)y1=﹣![]() x﹣
x﹣![]() ;(2)
;(2)![]() ;(3)当x<﹣4或0<x<2时,y1>y2.
;(3)当x<﹣4或0<x<2时,y1>y2.
【解析】
把点D(2,﹣3),点A(-2,0)代入![]() ,然后利用待定系数法求得一次函数的解析式;把点D(2,﹣3)代入
,然后利用待定系数法求得一次函数的解析式;把点D(2,﹣3)代入![]() ,利用待定系数法即可求得反比例函数的解析式;
,利用待定系数法即可求得反比例函数的解析式;
(2)联立两个解析式求得C的坐标,然后根据S△COD=S△AOC+S△AOD即可求得△COD的面积;
(3)根据图象即可求得.
解:(1)∵A(﹣2,0),D(2,﹣3)在y1=k1x+b的图象上,
∴![]() ,
,
解得k1=﹣![]() ,b=﹣
,b=﹣![]() ,
,
∴y1=﹣![]() x﹣
x﹣![]() ;
;
∵点D(2,﹣3)在反比例函数y2=![]() 的图象上,
的图象上,
∴k2=2×(﹣3)=﹣6,
∴y2=﹣![]() ;
;
(2)由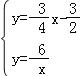 ,解得
,解得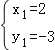 ,
,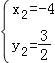 ,
,
∴C(﹣4,![]() ),
),
∴S△COD=S△AOC+S△AOD=![]() ×
×![]() +
+![]() ×2×3=
×2×3=![]() ;
;
(3)当x<﹣4或0<x<2时,y1>y2.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
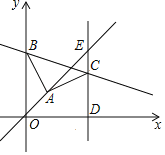
【题目】如图,平面直角坐标系中,![]() ,
,![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,在第一象限作
,在第一象限作![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,则直线
,则直线![]() 解析式为____________.
解析式为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC=BC,点D是BC上一点,∠ADE=∠C.
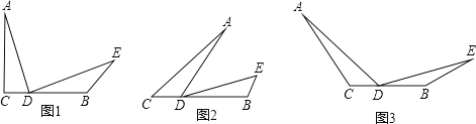
(1)如图1,若∠C=90°,∠DBE=135°.
①求证:∠EDB=∠CAD;
②求证:DA=DE;
(2)如图2,若∠C=40°,DA=DE,求∠DBE的度数;
(3)如图3,请直接写出∠DBE与∠C之间满足什么数量关系时,总有DA=DE成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副普通扑克牌中的4张;黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上.
(1)从中随机抽取一张牌是黑桃的概率是多少?
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形纸片ABCD中,AB=32cm,把长方形纸片沿AC折叠,点B落在点E处,AE交DC于点F,AF=25cm,则AD的长为( )
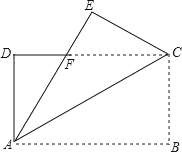
A. 16cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com