
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先求出△的值,再根据△的意义即可得到结论;
(2)先利用公式法求出方程的解为x1=2,x2=k-1,然后分类讨论当AB=BC或AC=BC时△ABC为等腰三角形,然后求出k的值.
解:(1)证明:△=b2-4ac=[-(k+1)]2-4×(2k-2)=k2-6k+9=(k-3)2,
∵(k-3)2≥0,即△≥0,
∴此方程总有两个实数根;
(2)解:一元二次方程x2-(k+1)x+2k-2=0的解为x=![]() ,即x1=2,x2=k-1,
,即x1=2,x2=k-1,
当AB=2,AC=k-1,且AB=AC时,△ABC是等腰三角形,则k-1=3,k=4,
当AB=2,AC=k-1,且AC=BC时,△ABC是等腰三角形,则k-1=2,解得k=3,
综合上述,k的值为3或4.


科目:初中数学 来源: 题型:
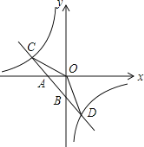
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是
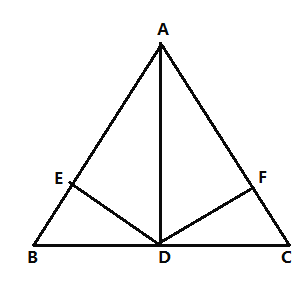
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
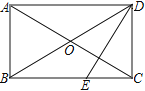
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
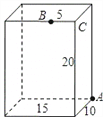
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com