
【题目】如图,在直角坐标系中,点![]() 的坐标是
的坐标是![]() ,抛物线
,抛物线![]() 经过原点
经过原点![]() 和点
和点![]() ,已知正方形
,已知正方形![]() 的三个顶点为
的三个顶点为![]() ,
,![]() ,
,![]() .
.
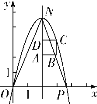
(1)若当![]() 时,求
时,求![]() ,
,![]() ,并写出抛物线对称轴及
,并写出抛物线对称轴及![]() 的最大值;
的最大值;
(2)求证:抛物线的顶点在函数![]() 的图象上;
的图象上;
(3)若抛物线与直线![]() 交于点
交于点![]() ,求
,求![]() 为何值时,
为何值时,![]() 的面积为1;
的面积为1;
(4)若抛物线经过正方形区域![]() (含边界),请直接写出
(含边界),请直接写出![]() 的取值范围.
的取值范围.
(参考公式:![]() 的顶点坐标是
的顶点坐标是 .
.
【答案】(1)![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,y最大值为4;(2)见解析;(3)当n的值为
,y最大值为4;(2)见解析;(3)当n的值为![]() 或1时,
或1时,![]() 的面积为1;(4)
的面积为1;(4)![]()
【解析】
(1)解:当![]() 时,则
时,则![]() ,
,
∵抛物线的![]() 经过原点O和点P,
经过原点O和点P,
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() ,
,
∴抛物线的对称轴为直线![]() ,
,
∵![]() ,
,
∴当![]() 时,y有最大值为4;
时,y有最大值为4;
(2)证明:把O、P的坐标代入抛物线解析式可得![]() ,
,
解得![]() ,
,
∴抛物线解析式为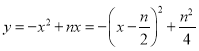 ,
,
∴抛物线顶点坐标为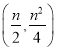 ,
,
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴抛物线的顶点在函数![]() 的图象上;
的图象上;
(3)解:在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点N的坐标为![]() ,
,
∴N到x轴的距离为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 的面积为1时,则有
的面积为1时,则有![]() ,
,
当![]() 时,N、P重合,不成立,
时,N、P重合,不成立,
当![]() 时,则
时,则![]() ,
,
解得![]() 或
或![]() (此时n小于2,舍去),
(此时n小于2,舍去),
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
综上可知,当n的值为![]() 或1时,
或1时,![]() 的面积为1;
的面积为1;
(4)解:![]() .
.
【解法提示】∵抛物线解析式为![]() ,
,
∴当过点![]() 时,代入可得
时,代入可得![]() ,解得
,解得![]() ,
,
同理,当抛物线过点B时可求得![]() ,
,
当抛物线过点C时可求得![]() ,
,
当抛物线过点D时可求得![]() ,
,
∴n的取值范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.
(1)在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;
(2)再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为![]() ,那么应添加多少张《消防知识手册》卡片?请说明理由.
,那么应添加多少张《消防知识手册》卡片?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河是中华民族的象征,被誉为母亲河,黄河壶口瀑布位于我省吉县城西45千米处,是黄河上最具气势的自然景观.其落差约30米,年平均流量1010立方米/秒.若以小时作时间单位,则其年平均流量可用科学记数法表示为( )

A. 6.06×104立方米/时 B. 3.136×106立方米/时
C. 3.636×106立方米/时 D. 36.36×105立方米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
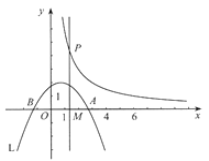
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象经过
的图象经过![]() ,与y轴交于点C,抛物线
,与y轴交于点C,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),交直线
与x轴交于点A,B(点A在点B的左侧),交直线![]() 于点P.
于点P.
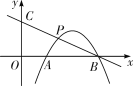
(1)若![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)若点P是线段![]() 的中点,求a的值;
的中点,求a的值;
(3)设点P的横坐标为![]() ,则当
,则当![]() 时,直接写出此时a的取值范围.
时,直接写出此时a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
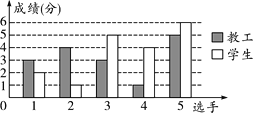
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
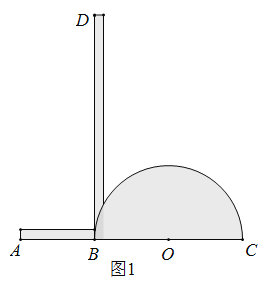
【题目】我们学习过利用用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的,人们根据实际需要,发明了一种简易操作工具--------三分角器.图1是它的示意图,其中![]() 与半圆
与半圆![]() 的直径
的直径![]() 在同一直线 上,且
在同一直线 上,且![]() 的长度与半圆的半径相等;
的长度与半圆的半径相等;![]() 与
与![]() 重直于点
重直于点 ![]() 足够长.
足够长.
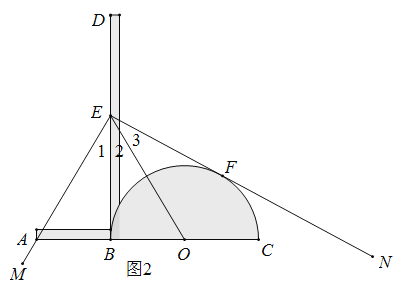
使用方法如图2所示,若要把![]() 三等分,只需适当放置三分角器,使
三等分,只需适当放置三分角器,使![]() 经过
经过![]() 的顶点
的顶点![]() ,点
,点![]() 落在边
落在边![]() 上,半圆
上,半圆![]() 与另一边
与另一边![]() 恰好相切,切点为
恰好相切,切点为![]() ,则
,则![]() 就把
就把![]() 三等分了.
三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点在![]() 同一直线上,
同一直线上,![]() 垂足为点
垂足为点![]() ,
,
求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com