
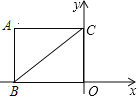
【题目】如图,平面直角坐标系中,矩形![]() 的边
的边![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,
轴上,![]() 点的坐标为
点的坐标为![]() ,点
,点![]() 在矩形
在矩形![]() 的内部,点
的内部,点![]() 在
在![]() 边上,满足
边上,满足![]() ∽
∽![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() 点坐标为_____.
点坐标为_____.
【答案】![]() 或
或![]()
【解析】
根据题意分情况讨论:①当![]() 点在
点在![]() 的垂直平分线上时,点
的垂直平分线上时,点![]() 同时在
同时在![]() 上,
上,![]() 的垂直平分线与
的垂直平分线与![]() 的交点即是
的交点即是![]() ,根据
,根据![]() ∽
∽![]() 求出PE,②
求出PE,②![]() 点在以点
点在以点![]() 为圆心
为圆心![]() 为半径的圆弧上,圆弧与
为半径的圆弧上,圆弧与![]() 的交点为
的交点为![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,根据
,根据![]() ∽
∽![]() ,求出
,求出![]() ,
,![]() ,则可得到
,则可得到![]() ,故而求出点
,故而求出点![]() 点坐标.
点坐标.
解:∵点![]() 在矩形
在矩形![]() 的内部,且
的内部,且![]() 是等腰三角形,
是等腰三角形,
∴![]() 点在
点在![]() 的垂直平分线上或在以点
的垂直平分线上或在以点![]() 为圆心
为圆心![]() 为半径的圆弧上;
为半径的圆弧上;
①当![]() 点在
点在![]() 的垂直平分线上时,点
的垂直平分线上时,点![]() 同时在
同时在![]() 上,
上,![]() 的垂直平分线与
的垂直平分线与![]() 的交点即是
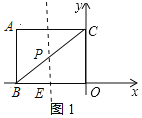
的交点即是![]() ,如图1所示:
,如图1所示:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∵四边形![]() 是矩形,
是矩形,![]() 点的坐标为
点的坐标为![]() ,
,
∴点![]() 横坐标为﹣4,
横坐标为﹣4,![]() ,
,![]() ,
,![]() ,
,
∵![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() ;
;
②![]() 点在以点
点在以点![]() 为圆心
为圆心![]() 为半径的圆弧上,圆弧与
为半径的圆弧上,圆弧与![]() 的交点为
的交点为![]() ,
,
过点![]() 作
作![]() 于
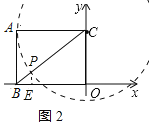
于![]() ,如图2所示:
,如图2所示:
∵![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∵四边形![]() 是矩形,
是矩形,![]() 点的坐标为
点的坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ∽
∽![]() ,
,
∴![]() ,即:
,即:![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() ;
;
综上所述:点![]() 的坐标为:
的坐标为:![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】温度的变化是人们经常谈论的话题,请根据下图解决下列问题.
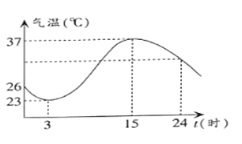
(1)这一天的最高温度是多少?是在几时到达的?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A(0,-2),B(-1,0),C(-5,0),点D从点B出发,沿x轴负方向运动到点C,E为AD上方一点,若在运动过程中始终保持△AED~△AOB,则点E运动的路径长为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)﹣(3)题
数学课上,老师出示了这样一道题:如图1,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() (其中
(其中![]() )
)![]() ,
,![]() 的平分线与
的平分线与![]() 相交于点
相交于点![]() ,
,![]() 垂足为
垂足为![]() ,探究线段
,探究线段![]() 与
与![]() 的数量关系,并证明.同学们经过思考后,交流了自已的想法:
的数量关系,并证明.同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段![]() 与
与![]() 的数量关系.”
的数量关系.”
……
老师:“保留原题条件,延长图1中的![]() ,与
,与![]() 相交于点
相交于点![]() (如图2),可以求出
(如图2),可以求出![]() 的值.”
的值.”
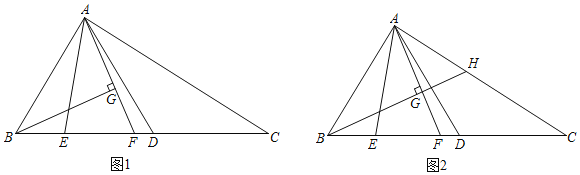
(1)求证:![]() ;
;
(2)探究线段![]() 与
与![]() 的数量关系(用含
的数量关系(用含![]() 的代数式表示),并证明;
的代数式表示),并证明;
(3)直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校在“我和我的祖国”快闪拍摄活动中,为学生化妆.其中5名男生和3名女生共需化妆费190元;3名男生的化妆费用与2名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为2000元,根据活动需要至少应有42名女生化妆,那么男生最多有多少人化妆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() ,交y轴于点
,交y轴于点![]() ,动点
,动点![]() 在对称轴上.
在对称轴上.
(1)求抛物线解析式;
(2)若点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向以1个单位/秒的速度匀速运动到点
方向以1个单位/秒的速度匀速运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交抛物线于点
交抛物线于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的面积最大?最大值是多少?
的面积最大?最大值是多少?
(3)若点![]() 是平面内的任意一点,在
是平面内的任意一点,在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得以点
,使得以点![]() 为顶点的四边形是菱形,若存在,请直接写出符合条件的
为顶点的四边形是菱形,若存在,请直接写出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
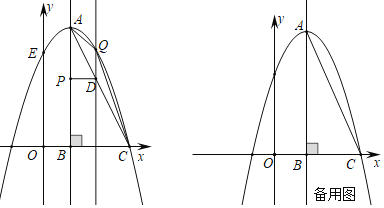
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
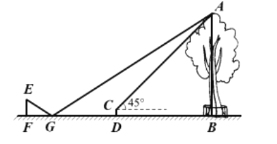
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组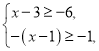
![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
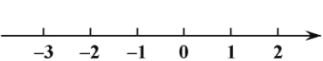
(Ⅳ)原不等式组的解集为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com