
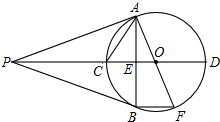
 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 首先连接OB,根据切线长定理得PA=PB,∠APO=∠BPO;易证得△APO≌△BPO,得∠AOP=∠BOP,即$\widehat{AC}=\widehat{BC}$;再根据这些基础条件进行判断即可.
解答 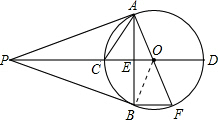 解:连接OB;
解:连接OB;
∵PA、PB都是⊙O的切线,
∴PA=PB,∠APO=∠BPO;
在△APO和△BPO中,
$\left\{\begin{array}{l}{PA=PB}\\{∠APO=∠BPO}\\{PO=PO}\end{array}\right.$,
∴△APO≌△BPO(SAS),
∴∠AOP=∠BOP,
∴$\widehat{AC}=\widehat{BC}$;
①∵PB切⊙O于点B,
∴∠PBA=∠AFB,
由$\widehat{AC}=\widehat{BC}$,得∠AFB=∠AOP,
∴∠PBA=∠AOP;
故①正确;
②∵∠AOC=∠BOC=∠FOD,
∴$\widehat{AC}=\widehat{BC}=\widehat{FD}$,
∴BC=DF,
故②正确;
③同①,可得∠PAB=∠AOC;
∵$\widehat{AC}=\widehat{BC}$,
∴∠AOC=∠BOC,
∴∠EAC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOC,
∴∠EAC=$\frac{1}{2}$∠PAB,
∴AC平分∠PAB,
∴∠PAC=$\frac{1}{2}$∠AOP,
故③正确;
④在△PEB和△ABF中,
$\left\{\begin{array}{l}{∠PEB=∠APF}\\{∠PBE=∠AFB}\end{array}\right.$,
∴△PEB∽△ABF,
∴BE:PE=BF:AB=BF:2BE,2BE2=$\frac{1}{2}$PE•BF,
故④正确;
综上所述,正确的结论共有4个;
故选A.
点评 此题主要考查的是切线的性质,涉及的知识点有:圆周角定理,全等三角形的判断和性质,切线长定理,圆心角、弧、弦的关系等,题目的综合性较强,对学生的综合能力要求很高,是一道不错的中考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 可以是a=-0.2,不可以是a=-2 | |
| B. | 可以是a=-2,不可以是a=-0.2 | |
| C. | 可以是a=-0.2,也可以是a=-2 | |
| D. | 既不可以是a=-0.2,也不可以是a=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
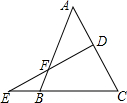 如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.
如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com