
【题目】已知二次函数的图像如图所示,下列结论:(1)a+b+c=0(2)a-b+c>0(3)abc>0(4)b=-2a;其中正确的结论个数有其中正确的个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
(1)由抛物线过点(1,0),即可得出a+b+c=0,结论(1)正确;(2)由当x=-1时,y>0,即可得出a-b+c>0,结论(2)正确;(3)由抛物线的开口方向、对称轴以及与y轴交点的位置,即可得出a<0、b<0、c>0,进而即可得出abc>0,结论(3)正确;(4)由抛物线对称轴为直线x=-1,即可得出b=2a,结论(4)错误.综上即可得出结论.
解:(1)∵点(1,0)在二次函数图象上,
∴a+b+c=0,结论(1)正确;
(2)∵当x=-1时,y>0,
∴a-b+c>0,结论(2)正确;
(3)∵抛物线开口向下,对称轴为直线x=-1,抛物线与y轴的交点在y轴正半轴,
∴a<0,-![]() =-1,c>0,
=-1,c>0,
∴a<0,b<0,c>0,
∴abc>0,结论(3)正确;
(4)∵抛物线对称轴为直线x=-1,
∴-![]() =-1,
=-1,
∴b=2a,结论(4)错误.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
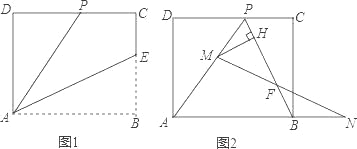
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
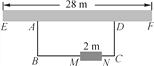
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形。

(1)求证AE=CG,并说明理由。
(2)连接AG,若AB=17,DG=13,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
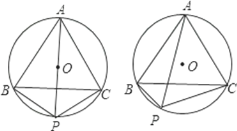
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为![]() ,则由题意列方程应为____________________________ 。
,则由题意列方程应为____________________________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com