
°æƒø°ø–°√˜∫Õ–°¿Ó◊º±∏∆þ‘¬≥ıµΩ÷ÿ«ÏªÚ≥§…≥»•¬√”Œ£¨Œ™¡À¡ÀΩ‚’‚¡Ω∏ˆ≥« –ƒƒ∏ˆ∏¸»»£¨À˚√«≤È‘ƒ◊ ¡œ£¨ ’ºØ¡À¡Ω∏ˆ≥« –2018ƒÍ∆þ‘¬«∞¡Ω÷Ð◊Ó∏þŒ¬∂»µƒº«¬º£¨»Áœ¬±Ì
»’∆⁄£®∆þ‘¬£© | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
÷ÿ«Ï◊Ó∏þŒ¬∂»/°Ê | 33 | 36 | 34 | 31 | 31 | 30 | 30 | 33 | 34 | 36 | 37 | 35 | 37 | 37 |
≥§…≥◊Ó∏þŒ¬∂»/°Ê | 29 | 34 | 35 | 35 | 36 | 29 | 31 | 31 | 34 | 35 | 35 | 31 | 35 | 35 |
∏˘æð…œ±Ì£¨À˚√«Ω´¡Ω∏ˆ≥« –µƒ◊Ó∏þŒ¬∂»∑÷±ªÊ÷∆¡À»Áœ¬µƒ∆µ ˝∑÷≤º÷±∑ΩÕº∫ÕÕ≥º∆±Ì£¨≤¢∂‘ ˝æðΩ¯––¡À’˚¿Ì
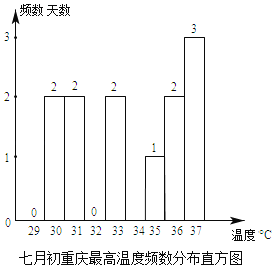
◊Ó∏þŒ¬∂»/°Ê | ÃÏ ˝ | ||||||
28°Ðx£º30 | 2 | ||||||
30°Ðx£º32 | a | ||||||
32°Ðx£º34 | 0 | ||||||
34°Ðx£º36 | 8 | ||||||
36°Ðx£º38 | 1 | ||||||
∆Ωæ˘ ˝/°Ê | ÷–Œª ˝/°Ê | ÷⁄ ˝/°Ê | 34°Ê“‘…œÃÏ ˝ | 30°Ê“‘œ¬ÃÏ ˝ | |||
÷ÿ«Ï | 33.9 | 34 | c | 6 | 0 | ||
≥§…≥ | 33.2 | b | 35 | 7 | 2 | ||
ªÿ¥»Áœ¬Œ Â
£®1£©±æ¥Œµ˜≤ȵƒƒøµƒ «°° °°£ª
£®2£©≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº≤¢–¥≥ˆ±Ì÷–a£¨b£¨cµƒ÷µ£¨a£Ω°° °°£¨b£Ω°° °°£¨c£Ω°° °°£ª
£®3£©Ω·∫œ“‘…œ∑÷Œˆ£¨ƒ„»œŒ™∆þ‘¬≥ıƒƒ∏ˆ≥« –∏¸»»£¨«Î–¥≥ˆ¡ΩÃı÷ß≥÷ƒ„π€µ„µƒ¿Ì”…£Æ
°æ¥∞∏°ø£®1£©±æ¥Œµ˜≤ȵƒƒøµƒ «£∫Œ™¡À¡ÀΩ‚’‚¡Ω∏ˆ≥« –ƒƒ∏ˆ∏¸»»£ª£®2£©º˚Ω‚Œˆ£ª3£¨35£¨37£ª£®3£©∆þ‘¬≥ı÷ÿ«Ï≥« –∏¸»»£¨¿Ì”…º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚ø…»∑∂®±æ¥Œµ˜≤ȵƒƒøµƒ£ª
£®2£©¿˚”√∆µ ˝∑÷≤º±Ì∫Õ∆µ ˝µƒ∫ÕŒ™14»∑∂®aµƒ÷µ£ª∏˘æð÷–Œª ˝∂®“»∑∂®bµƒ÷µ£ª∏˘æð÷⁄ ˝µƒ∂®“»∑∂®cµƒ÷µ£ª
£®3£©¥”∆Ωæ˘ ˝∫Õ÷⁄ ˝µƒ¥Û–°ø…≈–∂œ∆þ‘¬÷ÿ«Ï≥« –∏¸»»£Æ
Ω‚£∫£®1£©±æ¥Œµ˜≤ȵƒƒøµƒ «£∫Œ™¡À¡ÀΩ‚’‚¡Ω∏ˆ≥« –ƒƒ∏ˆ∏¸»»£ª
£®2£©≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº»ÁÕº£∫
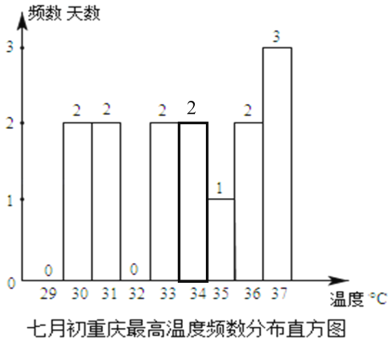
”…∆µ ˝∑÷≤º±Ìµ√a£Ω3£¨b£Ω35£¨
”…∆µ ˝∑÷≤º÷±∑ΩÕºµ√c£Ω37£ª
π ¥∞∏Œ™£∫Œ™¡À¡ÀΩ‚’‚¡Ω∏ˆ≥« –ƒƒ∏ˆ∏¸»»£ª3£¨35£¨37£ª
£®3£©∆þ‘¬≥ı÷ÿ«Ï≥« –∏¸»»£Æ
¿Ì”…»Áœ¬£∫∆þ‘¬≥ı÷ÿ«Ïµƒ◊Ó∏þŒ¬∂»µƒ∆Ωæ˘ ˝±»≥§…≥∏þ£ª∆þ‘¬≥ı÷ÿ«Ïµƒ◊Ó∏þŒ¬∂»µƒ÷⁄ ˝Œ™37£¨∂¯≥§…≥Œ™35°„£Æ


 ∆þ–«Õº Èø⁄À„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
∆þ–«Õº Èø⁄À„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏ ≥ı÷–—ß“µøº ‘µº”Ρ∑œµ¡–¥∞∏
≥ı÷–—ß“µøº ‘µº”Ρ∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæ“™π∫¬Ú“ª÷÷± º«±æπ©‘±π§—ßœ∞ ± π”√.‘⁄º◊ŒƒæþµÍ≤ªπГª¥Œπ∫¬Ú∂ý…Ÿ±æ£¨√ø±æº€∏ÒŒ™2‘™.‘⁄““ŒƒæþµÍπ∫¬ÚÕ¨—˘µƒ± º«±æ£¨“ª¥Œπ∫¬Ú ˝¡ø≤ª≥¨π˝20 ±£¨√ø±æº€∏ÒŒ™2.4‘™£ª“ª¥Œπ∫¬Ú ˝¡ø≥¨π˝20 ±£¨≥¨π˝≤ø∑÷√ø±æº€∏ÒŒ™1.8‘™.
…Ë‘⁄Õ¨“ªº“ŒƒæþµÍ“ª¥Œπ∫¬Ú’‚÷÷± º«±æµƒ ˝¡øŒ™x(xŒ™∑«∏∫’˚ ˝).
(¢Ò)∏˘æð“‚£¨ÃÓ–¥œ¬±Ì£∫
“ª¥Œπ∫¬Ú ˝¡ø(±æ) | 10 | 20 | 30 | 40 | °≠ |
º◊ŒƒæþµÍ∏∂øÓΩ∂Ó(‘™) | 20 | 60 | °≠ | ||
““ŒƒæþµÍ∏∂øÓΩ∂Ó(‘™) | 24 | 66 | °≠ |
(¢Ú)…Ë‘⁄º◊ŒƒæþµÍπ∫¬Ú’‚÷÷± º«±æµƒ∏∂øÓΩ∂ÓŒ™![]() ‘™£¨‘⁄““ŒƒæþµÍπ∫¬Ú’‚÷÷± º«±æµƒ∏∂øÓΩ∂ÓŒ™
‘™£¨‘⁄““ŒƒæþµÍπ∫¬Ú’‚÷÷± º«±æµƒ∏∂øÓΩ∂ÓŒ™![]() ‘™£¨∑÷±–¥≥ˆ
‘™£¨∑÷±–¥≥ˆ![]() £¨
£¨![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝πÿœµ Ω£ª
µƒ∫Ø ˝πÿœµ Ω£ª
(¢Û)µ±![]() ±£¨‘⁄ƒƒº“ŒƒæþµÍπ∫¬Ú’‚÷÷± º«±æµƒª®∑—…Ÿ£ø«ÎÀµ√˜¿Ì”….
±£¨‘⁄ƒƒº“ŒƒæþµÍπ∫¬Ú’‚÷÷± º«±æµƒª®∑—…Ÿ£ø«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() Œ™’˝’˚ ˝£Æ
Œ™’˝’˚ ˝£Æ
£®1£©÷§√˜£∫![]() ≤ªƒÐ±Ì 挙¡Ω∏ˆ“‘…œ¡¨–¯’˚ ˝µƒ≥Àª˝£ª
≤ªƒÐ±Ì 挙¡Ω∏ˆ“‘…œ¡¨–¯’˚ ˝µƒ≥Àª˝£ª
£®2£©»Ù![]() ƒÐ±Ì 挙¡Ω∏ˆ¡¨–¯’˚ ˝µƒ≥Àª˝£¨«Û
ƒÐ±Ì 挙¡Ω∏ˆ¡¨–¯’˚ ˝µƒ≥Àª˝£¨«Û![]() µƒ◊Ó¥Û÷µ£Æ
µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
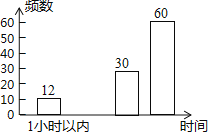
°æƒø°øƒ≥ –ΩÔ˝÷˜πÐ≤ø√≈Œ™¡ÀΩ‚—ß…˙µƒ◊˜“µ¡ø«Èøˆ£¨Àʪ˙≥È»°¡Àº∏À˘÷–—ß∞ÀƒÍº∂µƒ≤ø∑÷—ß…˙Ω¯––¡À“ª¥Œµ˜≤È£¨≤¢∏˘æð ’ºØµΩµƒ–≈œ¢Ω¯––¡ÀÕ≥º∆£¨ªÊ÷∆¡Àœ¬√Ê¡Ω∑˘…–≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«Îƒ„∏˘æðÕ≥º∆Õº°¢±Ì÷–À˘Ã·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®1£©±æ¥Œπ≤≥È»°¡À°° °°√˚—ß…˙Ω¯––µ˜≤È£ª
£®2£©x£Ω°° °°£¨y£Ω°° °°£¨≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©»Ù’‚º∏À˘÷–—ß∞ÀƒÍº∂µƒ—ß…˙π≤”–3200»À£¨«Îπ¿º∆◊ˆ◊˜“µ ±º‰‘⁄2–° ±“‘…œµƒ—ß…˙»À ˝ «∂ý…Ÿ£ø
£®4£©”…Õº±Ìø…÷™£¨’‚¥Œ±ªµ˜≤ȵƒ∞ÀƒÍº∂—ß…˙µƒ◊˜“µ ±º‰µƒ÷–Œª ˝“ª∂®¬‰‘⁄1.5–° ±©Å2–° ±’‚“ª ±∂Œƒ⁄£¨ƒ„»œŒ™’‚÷÷≈–∂œ’˝»∑¬£ø£®≤ª–Ë“™Àµ√˜¿Ì”…£©
–¥◊˜“µ ±º‰ | ∆µ ˝ | ∆µ¬ |
1–° ±“‘ƒ⁄ | 12 | 0.1 |
1©Å1.5 | x | 0.15 |
1.5©Å2 | 30 | 0.25 |
2–° ±“‘…œ | 60 | y |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨…Ω…œ”–“ª◊˘∏þÀ˛£¨…ΩΩ≈œ¬”–“ª‘≤÷˘–ŒΩ®÷˛ŒÔ∆Ω∏þÀ˛º∞…Ωµƒ∆ √ʔΑ≤÷˘–ŒΩ®÷˛ŒÔ∆Ω∆ √ÊABCD‘⁄Õ¨“ª∆Ω√Ê…œ£¨‘⁄µ„A¥¶≤‚µ√À˛∂•Hµƒ—ˆΩ«Œ™35°„£¨‘⁄µ„D¥¶≤‚µ√À˛∂•Hµƒ—ˆΩ«Œ™45°„£¨”÷≤‚µ√‘≤÷˘–ŒΩ®÷˛ŒÔµƒ…œµ◊√Ê÷±æ∂ADŒ™6m£¨∏þCDŒ™2.8m£¨‘ÚÀ˛∂•∂ÀHµΩµÿ√ʵƒ∏þ∂»HGŒ™£® £©
£®≤Œøº ˝æð£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £©
£©
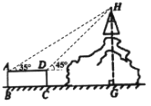
A.10.8mB.14mC.16.8mD.29.8m
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
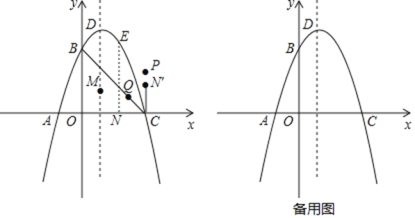
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµƒ⁄£¨≈◊ŒÔœþ![]() ”Îx÷·Ωª”⁄µ„A£¨C£®µ„A‘⁄µ„Cµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„B£¨∂•µ„Œ™D.µ„QŒ™œþ∂ŒBCµƒ»˝µ»∑÷µ„£®øøΩ¸µ„C£©.
”Îx÷·Ωª”⁄µ„A£¨C£®µ„A‘⁄µ„Cµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„B£¨∂•µ„Œ™D.µ„QŒ™œþ∂ŒBCµƒ»˝µ»∑÷µ„£®øøΩ¸µ„C£©.
£®1£©µ„MŒ™≈◊ŒÔœþ∂‘≥∆÷·…œ“ªµ„£¨µ„EŒ™∂‘≥∆÷·”“≤ý≈◊ŒÔœþ…œµƒµ„«“Œª”⁄µ⁄“ªœÛœÞ£¨µ±![]() µƒ÷Ð≥§◊Ó–° ±£¨«Û
µƒ÷Ð≥§◊Ó–° ±£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ£ª
√ʪ˝µƒ◊Ó¥Û÷µ£ª
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨µ±![]() µƒ√ʪ˝◊Ó¥Û ±£¨π˝µ„E◊˜
µƒ√ʪ˝◊Ó¥Û ±£¨π˝µ„E◊˜![]() ÷·£¨¥π◊„Œ™N£¨Ω´œþ∂ŒCN»∆µ„CÀ≥ ±’Ζ˝◊™90°„µ√µΩµ„N£¨‘ŸΩ´µ„NœÚ…œ∆Ω“∆
÷·£¨¥π◊„Œ™N£¨Ω´œþ∂ŒCN»∆µ„CÀ≥ ±’Ζ˝◊™90°„µ√µΩµ„N£¨‘ŸΩ´µ„NœÚ…œ∆Ω“∆![]() ∏ˆµ•Œª≥§∂».µ√µΩµ„P£¨µ„G‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ£¨«ÎŒ ‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµƒ⁄ «∑ҥʑ⁄“ªµ„H£¨ πµ„D£¨P£¨G£¨Hππ≥…¡‚–Œ.»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Hµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
∏ˆµ•Œª≥§∂».µ√µΩµ„P£¨µ„G‘⁄≈◊ŒÔœþµƒ∂‘≥∆÷·…œ£¨«ÎŒ ‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµƒ⁄ «∑ҥʑ⁄“ªµ„H£¨ πµ„D£¨P£¨G£¨Hππ≥…¡‚–Œ.»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Hµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø![]() ≥«”–∑ ¡œ
≥«”–∑ ¡œ![]() £¨
£¨![]() ≥«”–∑ ¡œ
≥«”–∑ ¡œ![]() .œ÷“™∞—’‚–©∑ ¡œ»´≤ø‘ÀÕ˘
.œ÷“™∞—’‚–©∑ ¡œ»´≤ø‘ÀÕ˘![]() °¢
°¢![]() ¡ΩœÁ£¨
¡ΩœÁ£¨![]() œÁ–Ë“™∑ ¡œ240t£¨
œÁ–Ë“™∑ ¡œ240t£¨![]() œÁ–Ë“™∑ ¡œ
œÁ–Ë“™∑ ¡œ![]() £¨∆‰‘ÀÕ˘
£¨∆‰‘ÀÕ˘![]() °¢
°¢![]() ¡ΩœÁµƒ‘À∑—»Áœ¬±Ì£∫
¡ΩœÁµƒ‘À∑—»Áœ¬±Ì£∫
¡Ω≥«/¡ΩœÁ | C/(‘™/ | D/(‘™/ |
| 20 | 24 |
| 15 | 17 |
…Ë¥”![]() ≥«‘ÀÕ˘
≥«‘ÀÕ˘![]() œÁµƒ∑ ¡œŒ™
œÁµƒ∑ ¡œŒ™![]() £¨¥”
£¨¥”![]() ≥«‘ÀÕ˘¡ΩœÁµƒ◊БÀ∑—Œ™
≥«‘ÀÕ˘¡ΩœÁµƒ◊БÀ∑—Œ™‘™£¨¥”
![]() ≥«‘ÀÕ˘¡ΩœÁµƒ◊БÀ∑—Œ™
≥«‘ÀÕ˘¡ΩœÁµƒ◊БÀ∑—Œ™![]() ‘™
‘™
(1)∑÷±–¥≥ˆ![]() °¢
°¢![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω(≤ª“™«Û–¥◊‘±‰¡øµƒ»°÷µ∑∂Œß)£ª
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω(≤ª“™«Û–¥◊‘±‰¡øµƒ»°÷µ∑∂Œß)£ª
(2) ‘±»Ωœ![]() °¢
°¢![]() ¡Ω≥«◊БÀ∑—µƒ¥Û–°£ª
¡Ω≥«◊БÀ∑—µƒ¥Û–°£ª
(3)»Ù![]() ≥«µƒ◊БÀ∑—≤ªµ√≥¨π˝4800‘™£¨‘ı—˘µ˜‘À π¡Ω≥«◊Ð∑—”√µƒ∫Õ◊Ó…Ÿ?≤¢«Û≥ˆ◊Ó–°÷µ£Æ
≥«µƒ◊БÀ∑—≤ªµ√≥¨π˝4800‘™£¨‘ı—˘µ˜‘À π¡Ω≥«◊Ð∑—”√µƒ∫Õ◊Ó…Ÿ?≤¢«Û≥ˆ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“þ«È∆⁄º‰£¨º◊°¢““¡Ω∏ˆø⁄’÷π§≥ßπ≤Õ¨≥–µ£ø⁄’÷…˙≤˙»ŒŒÒ£¨º◊π§≥ßµ•∂¿ÕÍ≥…¥ÀœÓ»ŒŒÒ±»““π§≥ßµ•∂¿ÕÍ≥…¥ÀœÓ»ŒŒÒ–Ë∂ý”√10ÃÏ£¨«“º◊π§≥ßµ•∂¿…˙≤˙45ÃÏ∫Õ““π§≥ßµ•∂¿…˙≤˙30Ãϵƒπ§◊˜¡øœýÕ¨£Æ
(1)º◊°¢““¡Ωπ§≥ßµ•∂¿ÕÍ≥…¥ÀœÓ»ŒŒÒ–Ë“™∂ý…ŸÃÏ£ø
(2)»Ùº◊°¢““¡Ωπ§≥ßπ≤Õ¨…˙≤˙¡À3ÃÏ∫Û£¨““π§≥ߓڅ˱∏ºÏ–ÞÕ£÷π…˙≤˙£¨”…º◊π§≥ߌ¨–¯…˙≤˙£¨Œ™¡À≤ª”∞œÏ»ŒŒÒΩ¯∂»£¨º◊π§≥ßµƒπ§◊˜–߬ ÷∏þµΩ‘≠¿¥µƒ2±∂£¨“™ πº◊π§≥ß◊еƒπ§◊˜¡ø≤ª…Ÿ”⁄““π§≥ß◊еƒπ§◊˜¡øµƒ2±∂£¨ƒ«√¥º◊π§≥ß–Ë“™÷¡…Ÿ‘Ÿµ•∂¿…˙≤˙∂ý…ŸÃÏ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
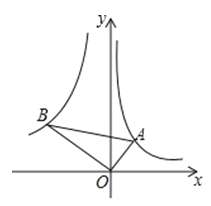
°æƒø°ø»ÁÕº£¨µ„![]() ∑÷±‘⁄∑¥±»¿˝∫Ø ˝
∑÷±‘⁄∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛ…œ£Æ»Ù
µƒÕºœÛ…œ£Æ»Ù![]() £¨
£¨![]() £¨‘Úµƒ÷µŒ™£® £©
£¨‘Úµƒ÷µŒ™£® £©
A.![]() B.
B.![]() C.4D.2
C.4D.2
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com