
分析 (1)、(2)、(3)、(4)根据二次根式的除法法则直接计算即可;
(5)先把带分数化为假分数,再根据二次根式的乘除法则进行计算即可;
(6)先把各根式化为最减二次根式,再根据二次根式的乘法法则进行计算即可.
解答 解:(1)原式=$\frac{\sqrt{3}}{\sqrt{64}}$=$\frac{\sqrt{3}}{8}$;
(2)原式=$\frac{\sqrt{64{b}^{2}}}{\sqrt{9{a}^{2}}}$
=$\frac{8b}{3a}$;
(3)原式=$\frac{\sqrt{9x}}{\sqrt{64{y}^{2}}}$
=$\frac{3\sqrt{x}}{8y}$;
(4)原式=$\frac{\sqrt{5x}}{\sqrt{169{y}^{2}}}$
=$\frac{\sqrt{5x}}{13y}$;
(5)原式=$\sqrt{\frac{5}{3}}$÷$\sqrt{\frac{7}{3}}$×$\sqrt{\frac{7}{5}}$
=$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$
=1;
(6)原式=2b$\sqrt{ab}$•(-$\frac{3a}{2}$$\sqrt{ab}$)
=-3ab$\sqrt{{a}^{2}{b}^{2}}$
=-3a2b2.
点评 本题考查的是分式的乘除法,熟知分式的乘法及除法法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
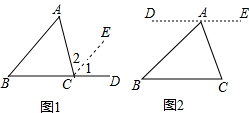 我们都知道“三角形的内角和等于180°”,如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的,请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整.
我们都知道“三角形的内角和等于180°”,如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的,请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com