

���� ��1����֤����ACP=��BCE��Ȼ������SAS֤����ACP�ա�BCE����ȫ�������ε����ʿɵõ�BE=AP��
��2������C��CH��BE������ΪH�������ݵ������������ߺ�һ��������á�CAD=30�㣬Ȼ���ɡ�ACP�ա�BCE����á�CBH=30�㣬���ݺ�30��ֱ�������ε����ʿ����CH�ij����Ӷ������BH�ij���Ȼ���ڡ�ECH�����ݹ��ɶ��������EH�ij����ʴ˿����BE�ij���������AP=BE��⼴�ɣ�
��3�����ȸ������⻭��ͼ�Σ�����C��CH��BE������ΪH����֤��ACP�ա�BCE���Ӷ��õ���CBH=30�㣬�ɺ�30��ֱ�������ε����ʿ����CH�ij������ݹ��ɶ��������FH�ij���Ȼ���ɵ������������ߺ�һ�����ʿɵõ�HE=FH���ʴ˿����EF�ij���
��� �⣺��1��BE=AP��
���ɣ��ߡ�ABC�͡�CPE��Ϊ�ȱ������Σ�
���ACB=��PCE=60�㣬AC=BC��CP=CE��
�ߡ�ACP+��DCP=��DCE+��PCD=60�㣬
���ACP=��BCE��
���ڡ�ACP�͡�BCE�У�$\left\{\begin{array}{l}{AC=BC}\\{��ACP=��BCE}\\{PC=EC}\end{array}\right.$��
���ACP�ա�BCE��
��BE=AP��
��2����ͼ2��ʾ������C��CH��BE������ΪH��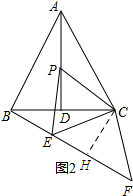
��AB=AC��AD��BC���е㣬
���CAD=��BAD=$\frac{1}{2}$��BAC=30�㣮
���ɣ�1����֪����ACP�ա�BCE��
���CBE=��CAD=30�㣬AP=BE��
����Rt��BCH�У���HBC=30�㣬
��HC=$\frac{1}{2}$BC=3��NH=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$��
����Rt��CEH��EC=5��CH=3��
��EH=$\sqrt{C{E}^{2}-C{H}^{2}}$=4��
��BE=HB-EH=3$\sqrt{3}$-4��
��A=3$\sqrt{3}$-4��
��3����ͼ3��ʾ������C��CH��BE������ΪH��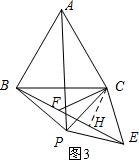
�ߡ�ABC�͡�CEP��Ϊ�ȱ������Σ�
��AC=BC��CE=PC����ACB=��ECP��
���ACB+��BCP=��ECP+BCP������BCE=��ACP��
���ڡ�ACP�͡�BCE�У�$\left\{\begin{array}{l}{AC=BC}\\{��ACP=��BCE}\\{PC=CE}\end{array}\right.$��
���ACP�ա�BCE��
���CBH=��CAP=30�㣮
����Rt��BCH�У���CBH=30�㣬
��HC=$\frac{1}{2}$BC=3��
��FC=CE��CH��FE��
��FH=EH��
��FH=EH=$\sqrt{C{E}^{2}-H{C}^{2}}$=4��
��EF=FH+EH=4+4=8��
���� ������Ҫ�������ȫ�������ε����ʺ��ж������ɶ�����Ӧ�á��ȱ������ε����ʡ���30�������ε����ʣ�֤�á�ACP�ա�BCE�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
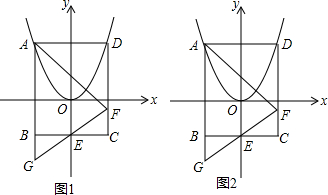
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
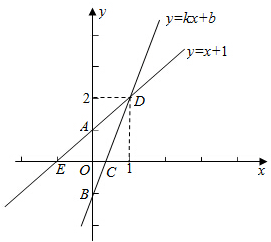 ��ͼ����ֱ֪��y=x+1��y�ύ�ڵ�A��һ�κ���y=kx+b��ͼ����B��0��-1����������x���Լ�ֱ��y=x+1�ֱ��ڵ�C��D��
��ͼ����ֱ֪��y=x+1��y�ύ�ڵ�A��һ�κ���y=kx+b��ͼ����B��0��-1����������x���Լ�ֱ��y=x+1�ֱ��ڵ�C��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-��x+3��2+1 | B�� | y=-��x+1��2+3 | C�� | y=-��x-1��2+4 | D�� | y=-��x+1��2+4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com