
分析 (1)首先把括号里的式子进行通分,然后把除法运算转化成乘法运算,进行约分化简;
(2)先求解不等式,再根据已知条件即可得出答案.
解答 解:(1)$\frac{x+1}{x}$÷(x-$\frac{1{+x}^{2}}{2x}$)
=$\frac{x+1}{x}$÷$\frac{2{x}^{2}-1-{x}^{2}}{2x}$
=$\frac{x+1}{x}$×$\frac{2x}{(x+1)(x-1)}$
=$\frac{2}{x-1}$;
(2)2x-6>$\frac{1}{3}$a,
2x>6+$\frac{1}{3}$a,
x>3+$\frac{1}{6}$a,
∵解集为x>-1,
∴3+$\frac{1}{6}$a=-1,
解得a=-24.
点评 考查了分式的混合运算,通分、因式分解和约分是解答的关键.同时考查了解一元一次不等式,属于基础题,关键是掌握不等式的基本性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )
如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )| A. | 4$\sqrt{2}$ | B. | 5$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 区县 | 宣威 | 富源 | 沾益 | 马龙 | 师宗 | 罗平 | 陆良 | 会泽 | 麒麟区 | 经开区 |
| 可吸入颗粒物 (mg/m3) | 0.18 | 0.18 | 0.15 | 0.13 | 0.14 | 0.13 | 0.15 | 0.15 | 0.15 | 0.14 |
| A. | 0.15和0.14 | B. | 0.18和0.15 | C. | 0.18和0.14 | D. | 0.15和0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
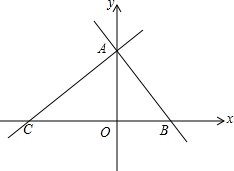 如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).
如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com