
分析 (1)根据特殊值法,可得规律:0<a<1,则比较$\frac{1}{a}$>$\frac{1}{{a}^{2}}$;可得答案.
(2)根据特殊值法,可得规律:当-1<a<0时,a>$\frac{1}{a}$;当a≤-1时,a≤$\frac{1}{a}$.
解答 解:(1)如$\frac{1}{2}$>$\frac{1}{4}$=$\frac{1}{{2}^{2}}$,$\frac{1}{3}$$>\frac{1}{{3}^{2}}$=$\frac{1}{9}$,$\frac{1}{4}$$>\frac{1}{{4}^{2}}$=$\frac{1}{16}$,
0<a<1,则比较$\frac{1}{a}$>$\frac{1}{{a}^{2}}$;
(2)a=-$\frac{1}{2}$,$\frac{1}{a}$=-2,a>$\frac{1}{a}$;a=-0.25=-$\frac{1}{4}$,$\frac{1}{a}$=-4,a>$\frac{1}{a}$,
当-1<a<0时,a>$\frac{1}{a}$;
a=-2,$\frac{1}{a}$=-$\frac{1}{2}$,$\frac{1}{a}$>a;a=-1,$\frac{1}{a}$=-1;a=-5,$\frac{1}{a}$=-$\frac{1}{5}$,$\frac{1}{a}$>a,
当a≤-1时,a≤$\frac{1}{a}$.
点评 本题考查了有理数的大小比较,利用特殊值法得出规律是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
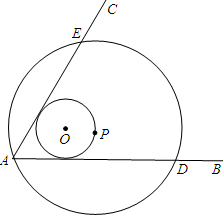 如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.
如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com