
分析 (1)只要证明△>0即可.
(2)把条件|x1|=|x2|-2转化为x1+x2与x1x2的形式即可.
解答 (1)证明:∵△=(m-3)2+4>0,
∴方程总有两个不相等的实数根.
(2)∵|x1|=|x2|-2
∴|x1|-|x2|=-2
∴x12-2|x1x2|+x22=4
∴(x1+x2)2-2x1x2=6
∵x1+x2=m-3,x1x2=-1,
∴(m-3)2=4,
∴m-3=±2,
m=5或1
当m=5时,方程为:x2-2x-1=0,解得x=1$±\sqrt{2}$,
当m=1时,方程为:x2+2x-1=0,解得x=-1$±\sqrt{2}$
点评 本题考查根与系数的关系、根的判别式等知识,把|x1|=|x2|-2转化为x1+x2与x1x2的形式是一个难点,灵活运用公式是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
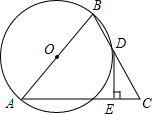 已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.
已知,如图,△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A、B、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
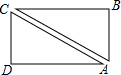 传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?
传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com