
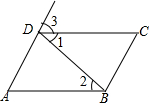
 如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有①②⑤.(只填序号)
如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有①②⑤.(只填序号)分析 ①由在△ABC中,AB=AC,BD=DC,根据三线合一的性质,可得∠BAD=∠CAD,AD⊥BC,然后由角平分线的性质,证得结论;
②由中线的性质,可证得S△ABD=S△ACD=2S△DCE;
③由∠BAC不一定等于90°,可得四边形AMPF不一定是正方形;
④由BP不是角平分线,可得∠BPD≠∠BPM;
⑤易证得△APM∽△BPD,然后由相似三角形的对应边成比例,证得结论.
解答 解:①∵在△ABC中,AB=AC,BD=DC,
∴∠BAD=∠CAD,AD⊥BC,
∵BF⊥AC,PM⊥AB,
∴PM=PF;故正确;
②∵BD=DC,
∴S△ABD=S△ACD;
∵DE∥AB,
∴E是AC的中点,
∴S△ABD=S△ACD=2S△DCE;故正确;
③∵∠BAC不一定为直角,
∴四边形AMPF不一定是正方形;故错误;
④∵BF不是角平分线,
∴∠ABP≠∠DBP,
∵∠BMP=∠BDP=90°,
∴∠BPM≠∠BPD;故错误;
⑤∵∠AMP=∠BDP=90°,
又∵∠APM=∠APF=∠BPD,
∴△APM∽△BPD,
∴$\frac{AM}{BD}$=$\frac{AP}{BP}$.故正确.
故答案为:①②⑤.
点评 此题考查了相似三角形的判定与性质、等腰三角形的性质以及正方形的判定.注意掌握等腰三角形三线合一的性质是关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
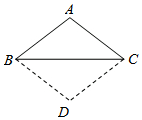 如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )| A. | 一组邻边相等的平行四边形是菱形 | |
| B. | 四条边相等的四边形是菱形 | |
| C. | 对角线互相垂直的平行四边形是菱形 | |
| D. | 对角线互相垂直的平分四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=2 | B. | a=0,b=0 | C. | a=3,b=-2 | D. | a=-3,b=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 推理填空:
推理填空:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com