Question

10．如图1，在平面直角坐标系中，抛物线 y=$\frac{\sqrt{3}}{3}$x²-$\frac{8}{3}$x-$\sqrt{3}$与x轴交于A、B、两点（点A在点B的左侧），与y轴交于点C．
（1）判断△ABC形状，并说明理由．
（2）在抛物线第四象限上有一点，它关于x轴的对称点记为点P，点M是直线BC上的一动点，当△PBC的面积最大时，求PM+$\frac{\sqrt{10}}{10}$MC的最小值；
（3）如图2，点K为抛物线的顶点，点D在抛物线对称轴上且纵坐标为$\sqrt{3}$，对称轴右侧的抛物线上有一动点E，过点E作EH∥CK，交对称轴于点H，延长HE至点F，使得EF=$\frac{5\sqrt{3}}{3}$，在平面内找一点Q，使得以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴，请问是否存在这样的点Q，若存在请直接写出点E的横坐标，若不存在，请说明理由．

Answer 1

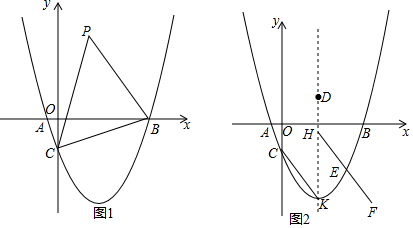
分析 （1）结论：△ABC是直角三角形．由△AOC∽△COB，推出∠ACO=∠OBC，由∠OBC+∠OCB=90°，推出∠ACO+∠BCO=90°，推出∠ACB=90°．（也可以求出AC、BC、AB利用勾股定理的逆定理证明）．
（2）如图1中，设第四象限抛物线上一点N（m，$\frac{\sqrt{3}}{3}$m²-$\frac{8}{3}$m-$\sqrt{3}$），点N关于x轴的对称点P（m，-$\frac{\sqrt{3}}{3}$m²+$\frac{8}{3}$m+$\sqrt{3}$），作过B、C分别作y轴，x轴的平行线交于点G，连接PG．
可得S_△PBC=S_△PCG+S_△PBG-S_△BCG=$\frac{1}{2}$×$3\sqrt{3}$×（-$\frac{\sqrt{3}}{3}$m²+$\frac{8}{3}$m+2$\sqrt{3}$）+$\frac{1}{2}$×$\sqrt{3}$•（3$\sqrt{3}$-m）-$\frac{1}{2}$×$3\sqrt{3}$×$\sqrt{3}$=-$\frac{3}{2}$（m-$\frac{7\sqrt{3}}{6}$）²+$\frac{121}{8}$．由此可得△PBC面积最大时的点P的坐标，如图2中，作ME⊥CG于M．由△CEM∽△BOC，OC：OB：BC=1：3：$\sqrt{10}$，推出EM：CE：CM=1：3：$\sqrt{10}$，推出EM=$\frac{\sqrt{10}}{10}$CM，所以PM+$\frac{\sqrt{10}}{10}$CM=PM+ME，所以根据垂线段最短可知，当PE⊥CG时，PM+ME最短，由此即可解决问题．
（3）分三种情形讨论①如图3中，当DH=HF，HQ平分∠DHF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．②如图4中，当DH=HF，HQ平分∠DHF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．③如图5中，当DH=DF，DQ平分∠HDF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．分别列出方程求解即可．

解答 解：（1）结论：△ABC是直角三角形．理由如下，
对于抛物线 y=$\frac{\sqrt{3}}{3}$x²-$\frac{8}{3}$x-$\sqrt{3}$，令y=0得 $\frac{\sqrt{3}}{3}$x²-$\frac{8}{3}$x-$\sqrt{3}$=0，解得x=-$\frac{\sqrt{3}}{3}$或3$\sqrt{3}$；令x=0得y=-$\sqrt{3}$，
∴A（-$\frac{\sqrt{3}}{3}$，0），C（0，-$\sqrt{3}$），B（3$\sqrt{3}$，0），
∴OA=$\frac{\sqrt{3}}{3}$，OC=$\sqrt{3}$，OB=3$\sqrt{3}$，
∴$\frac{AO}{OC}$=$\frac{OC}{OB}$=$\frac{1}{3}$，∵∠AOC=∠BOC，
∴△AOC∽△COB，
∴∠ACO=∠OBC，
∵∠OBC+∠OCB=90°，
∴∠ACO+∠BCO=90°，
∴∠ACB=90°．
（也可以求出AC、BC、AB利用勾股定理的逆定理证明）．

（2）如图1中，设第四象限抛物线上一点N（m，$\frac{\sqrt{3}}{3}$m²-$\frac{8}{3}$m-$\sqrt{3}$），点N关于x轴的对称点P（m，-$\frac{\sqrt{3}}{3}$m²+$\frac{8}{3}$m+$\sqrt{3}$），作过B、C分别作y轴，x轴的平行线交于点G，连接PG．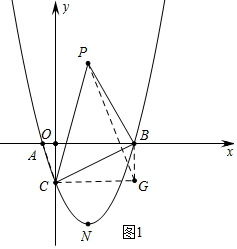

∵G（3$\sqrt{3}$，-$\sqrt{3}$），
∴S_△PBC=S_△PCG+S_△PBG-S_△BCG=$\frac{1}{2}$×$3\sqrt{3}$×（-$\frac{\sqrt{3}}{3}$m²+$\frac{8}{3}$m+2$\sqrt{3}$）+$\frac{1}{2}$×$\sqrt{3}$•（3$\sqrt{3}$-m）-$\frac{1}{2}$×$3\sqrt{3}$×$\sqrt{3}$=-$\frac{3}{2}$（m-$\frac{7\sqrt{3}}{6}$）²+$\frac{121}{8}$．
∵-$\frac{3}{2}$＜0，
∴当m=$\frac{7\sqrt{3}}{6}$时，△PBC的面积最大，
此时P（$\frac{7\sqrt{3}}{6}$，$\frac{11\sqrt{3}}{4}$），
如图2中，作ME⊥CG于M．

∵CG∥OB，
∴∠OBC=∠ECM，∵∠BOC=∠CEM，
∴△CEM∽△BOC，
∵OC：OB：BC=1：3：$\sqrt{10}$，
∴EM：CE：CM=1：3：$\sqrt{10}$，
∴EM=$\frac{\sqrt{10}}{10}$CM，
∴PM+$\frac{\sqrt{10}}{10}$CM=PM+ME，
∴根据垂线段最短可知，当PE⊥CG时，PM+ME最短，
∴PM+$\frac{\sqrt{10}}{10}$MC的最小值为$\frac{11\sqrt{3}}{4}$+$\sqrt{3}$=$\frac{15\sqrt{3}}{4}$．

（3）存在．理由如下，
①如图3中，当DH=HF，HQ平分∠DHF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．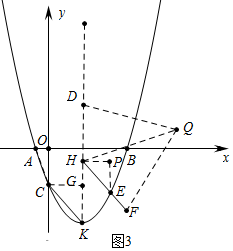

作CG⊥HK于G，PH∥x轴，EP⊥PH于P．
∵FH∥CK，K（$\frac{4}{3}$$\sqrt{3}$，-$\frac{25}{9}$$\sqrt{3}$），
易知CG：GK：CK=3：4：5，
由△EPH∽△KGC，得PH：PE：EH=3：4：5，设E（（n，$\frac{\sqrt{3}}{3}$n²-$\frac{8}{3}$n-$\sqrt{3}$），则HE=$\frac{5}{3}$（n-$\frac{4}{3}$$\sqrt{3}$），PE=$\frac{4}{3}$（n-$\frac{4}{3}$$\sqrt{3}$），
∵DH=HF，
∴$\sqrt{3}$+[-$\frac{\sqrt{3}}{3}$n²+$\frac{8}{3}$n+$\sqrt{3}$-$\frac{4}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）]=$\frac{5}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）+$\frac{5}{3}$$\sqrt{3}$，
解得n=$\frac{-\sqrt{3}+\sqrt{471}}{6}$或$\frac{-\sqrt{3}-\sqrt{471}}{6}$（舍弃）．
②如图4中，当DH=HF，HQ平分∠DHF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．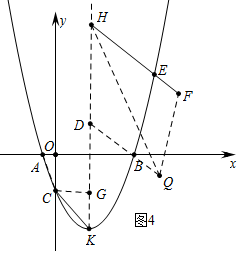

同法可得[$\frac{\sqrt{3}}{3}$n²-$\frac{8}{3}$n-$\sqrt{3}$+$\frac{4}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）]-$\sqrt{3}$=$\frac{5}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）+$\frac{5}{3}$$\sqrt{3}$，
解得n=$\frac{3\sqrt{3}}{2}$+$\frac{\sqrt{591}}{6}$或$\frac{3\sqrt{3}}{2}$-$\frac{\sqrt{591}}{6}$（舍弃）．
③如图5中，当DH=DF，DQ平分∠HDF时，以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴．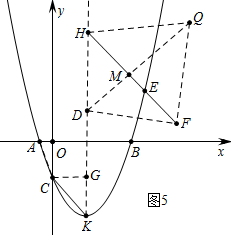

设DQ交HF于M．由△DHM∽△CKG，可知HM：DH=4：5，
$\frac{1}{2}$[$\frac{5}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）+$\frac{5}{3}$$\sqrt{3}$]：[$\frac{\sqrt{3}}{3}$n²-$\frac{8}{3}$n-$\sqrt{3}$+$\frac{4}{3}$（n-$\frac{4}{3}$$\sqrt{3}$）-$\sqrt{3}$]=4：5，
解得n=$\frac{19\sqrt{3}}{16}$+$\frac{\sqrt{33459}}{48}$或=$\frac{19\sqrt{3}}{16}$-$\frac{\sqrt{33459}}{48}$（舍弃），
综上所，满足条件的点E的横坐标为$\frac{-\sqrt{3}+\sqrt{471}}{6}$或$\frac{3\sqrt{3}}{2}$+$\frac{\sqrt{591}}{6}$或$\frac{19\sqrt{3}}{16}$+$\frac{\sqrt{33459}}{48}$．

点评 本题考查二次函数综合题、相似三角形的判定和性质、勾股定理、垂线段最短等知识，解题的关键是灵活运用所学知识，学会构建二次函数解决最值问题，学会利用垂线段最短解决最值问题，学会用分类讨论的思想思考问题，属于中考压轴题．