
【题目】(1)已知有一条抛物线的形状(开口方向和开口大小)与抛物线y=2x![]() 相同,它的对称轴是直线x=2;且当x=1时,y=6,求这条抛物线的解析式。
相同,它的对称轴是直线x=2;且当x=1时,y=6,求这条抛物线的解析式。
(2)定义:如果点P(t,t)在抛物线上,则点P叫做这条抛物线的不动点。
①求出(1)中所求抛物线的所有不动点的坐标;
②当a、b、c满足什么关系式时,抛物线y=ax![]() +bx+c上一定存在不动点。
+bx+c上一定存在不动点。
【答案】(l)y=2x![]() +8x4;(2)①P
+8x4;(2)①P![]() (
(![]() ,
,![]() ),P
),P![]() (4,4).②当△=(b1)
(4,4).②当△=(b1) ![]() 4ac0时,抛物线上一定存在不动点.
4ac0时,抛物线上一定存在不动点.
【解析】
(1)设抛物线的解析式为y=ax![]() +bx+c,由题意代入数值求出a,b,c即可;
+bx+c,由题意代入数值求出a,b,c即可;
(2)①设P(t,t)是抛物线的不动点,则2t![]() +8t-4=t解得t的值,求得点P坐标;
+8t-4=t解得t的值,求得点P坐标;
②设P(t,t)是抛物线的不动点,则at![]() +bt+c=t分两种情况讨论:当(b-1)
+bt+c=t分两种情况讨论:当(b-1)![]() -4ac≥0时,这个方程有实数解;当△=(b-1)
-4ac≥0时,这个方程有实数解;当△=(b-1)![]() -4ac≥0时,抛物线上一定存在不动点.
-4ac≥0时,抛物线上一定存在不动点.
(1)设抛物线的解析式为y=ax![]() +bx+c(a≠0)
+bx+c(a≠0)
由已知可得a=2,∴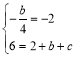 .
.
解得:b=8,c=4
∴抛物线的解析式为y=2x![]() +8x4
+8x4
(2)①设P(t,t)是抛物线的不动点,则2t![]() +8t4=t
+8t4=t
解得:t![]() =
=![]() ,t
,t![]() =4,∴不动点P
=4,∴不动点P![]() (
(![]() ,
,![]() ),P
),P![]() (4,4)
(4,4)
②设P(t,t)是抛物线的不动点,则at+bt+c=t
∴at![]() +(b1)t+c=0
+(b1)t+c=0
∴当(b1) ![]() 4ac0时,这个方程有实数解,
4ac0时,这个方程有实数解,
∴当△=(b1) ![]() 4ac0时,抛物线上一定存在不动点.
4ac0时,抛物线上一定存在不动点.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CBA=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
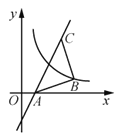
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
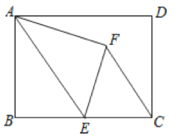
【题目】如图,四边形ABCD为矩形,AB=4,BC=6,点E是BC边的中点,将△ABE沿直线AE折叠,点B落在点F处,连接CF,则sin∠ECF的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+3x+1=0有两个不相等的实数根,则m的取值范围为( )
A. m<![]() B. m<
B. m<![]() 且m≠0C. m≤
且m≠0C. m≤![]() D. m≤
D. m≤![]() 且m≠0
且m≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
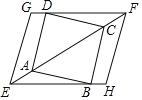
【题目】如图,在正方形ABCD中,分别过顶点B,D作![]() 交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使
交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使![]() ,连接EG,FH.
,连接EG,FH.
(1)求证:四边形EHFG是平行四边形;
(2)已知:![]() ,
,![]() ,
,![]() ,求四边形EHFG的周长.
,求四边形EHFG的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com