
【题目】点![]() 是
是![]() 边上的点,点
边上的点,点![]() 是边
是边![]() 的中点,
的中点,![]() 平分
平分![]() 的面积,若
的面积,若![]() ,
,![]() ,
,![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
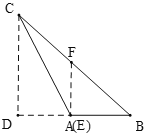
如图,由点F是边BC的中点,EF平分△ABC的面积可得点E与点A重合,过点C作CD⊥AB,交BA延长线于D,连接AF,由∠BAC=120°可得∠DAC=60°,根据含30°角的直角三角形的性质可求出CD、AD的长,可得AD=AB,即可证明AF为△CDB的中位线,根据三角形中位线的性质即可得答案.
如图,过点C作CD⊥AB,交BA延长线于D,连接AF,
∵由点F是边BC的中点,EF平分△ABC的面积,
∴点E与点A重合,
∵∠BAC=120°,
∴∠DAC=180°-120°=60°,
∴∠DCA=30°,
∵AC=4,∠CDA=90°,
∴AD=![]() AC=2,CD=
AC=2,CD=![]() =2
=2![]() ,
,
∵AB=2,
∴AD=AB,
∵F为BC中点,
∴AF是△CDB的中位线,
∴AF=![]() CD=
CD=![]() ,即EF=
,即EF=![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
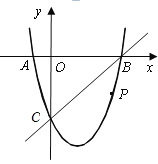
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知: ![]() .
.

求作: ![]() 边上的高
边上的高![]()
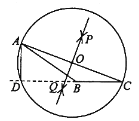
作法:如图,
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
, ![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心, ![]() 为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
请回答;该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com