
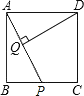
【题目】如图,在正方形ABCD中,AB=2,P是BC边上与B、C不重合的任意一点,DQ⊥AP于点Q
(1)判断△DAQ与△APB是否相似,并说明理由.
(2)当点P在BC上移动时,线段DQ也随之变化,设PA=x,DQ=y,求y与x间的函数关系式,并求出x的取值范围.
【答案】(1)△DAQ∽△APB,见解析;(2)y=![]() ,2<x<2
,2<x<2![]()
【解析】
(1)根据四边形ABCD是正方形,得AD∥BC,∠B=90°,∠DAP=∠APB,根据DQ⊥AP,得∠B=∠AQD,即可证出△DAQ∽△APB;
(2)根据△DAQ∽△APB,得![]() ,再把AB=2,DA=2,PA=x,DQ=y代入得出
,再把AB=2,DA=2,PA=x,DQ=y代入得出![]() ,y=
,y=![]() .根据点P在BC上移到C点时,PA最长,求出此时PA的长即可得出x的取值范围.
.根据点P在BC上移到C点时,PA最长,求出此时PA的长即可得出x的取值范围.
解:(1)∵四边形ABCD是正方形,
∴AD∥BC,∠B=90°,
∴∠DAP=∠APB,
∵DQ⊥AP,
∴∠AQD=90°,
∴∠B=∠AQD,
∴△DAQ∽△APB;
(2)∵△DAQ∽△APB,
∴![]() ,
,
∵AB=2,四边形ABCD是正方形,
∴DA=2,
∵PA=x,DQ=y,
∴![]() ,
,
∴y=![]() .
.
∵点P在BC上移到C点时,PA最长,此时PA=![]() ,
,
又∵P是BC边上与B、C不重合的任意一点,
∴x的取值范围是;2<x<2![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连接OD,AC.
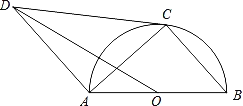
(1)求证:△ABC∽△DCA;
(2)若AC=2![]() ,BC=4,求DO的长.
,BC=4,求DO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)~(3)题.
数学课上,老师出示了这样一道题:
如图1,△ABC中,AC=BC=a,∠ACB=90°,点D在AB上,且AD=kAB(其中0<k<![]() ),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现DC与DE相等”;
小伟:“通过构造全等三角形,经过进一步推理,可以得到DC与DE相等”
小强:“通过进一步的推理计算,可以得到BE与BC的数量关系”
老师:“保留原题条件,连接CE交AB于点O.如果给出BO与DO的数量关系,那么可以求出COEO的值”
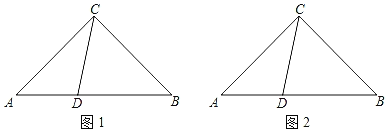
(1)在图1中将图补充完整,并证明DC=DE;
(2)直接写出线段BE与BC的数量关系 (用含k的代数式表示);
(3)在图2中将图补充完整,若BO=![]() DO,求COEO的值(用含a的代数式表示).
DO,求COEO的值(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张不透明的卡片,除正面上的图案不同外,其他均相同,将这4张卡片背面向上洗匀后放在桌面上.
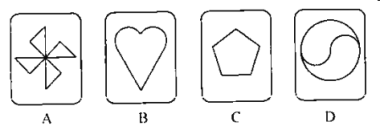
(1)从中随机油取1张卡片,卡片上的图案是中心对称图形的概率为_________;
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用列表的方法,求两次所抽取的卡片恰好都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
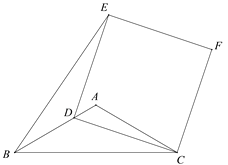
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
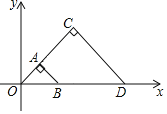
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:3,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
A.(3,3)B.(2,4)C.(![]() ,2
,2![]() )D.(4,4)
)D.(4,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
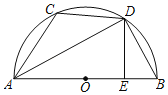
【题目】如图,四边形ABDC内接于半圆O,AB为直径,AD平分∠CAB,AB﹣AC=4,AD=3![]() ,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com