

分析 连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,由点F,点G关于直线DE的对称,得到DF=DG,根据正方形的性质得到AD=CD,∠ADC=∠A=∠BCD=90°,推出Rt△AFD≌Rt△CDG,证得△FDG是等腰直角三角形,推出四边形APHQ是矩形,证得△HPF≌△DHQ,根据全等三角形的性质得到HP=HQ,证得APHQ为正方形,利用正方形性质联系题中所给数据计算出正方形边长,然后再利用△FPH∽△EHG求得EG长.
解答 解:连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,
∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,$\left\{\begin{array}{l}{AD=CD}\\{DF=DG}\end{array}\right.$,
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
∴DH=FH=$\frac{1}{2}$FG,
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,又在△PFF与△DQH中有$\left\{\begin{array}{l}{∠HPF=∠HQD=90°}\\{∠PHF=∠DHQ}\\{HF=HD}\end{array}\right.$,
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,则有$\frac{EG}{FH}=\frac{GH}{PH}$,即EG=$\frac{F{H}^{2}}{PH}$,
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,勾股定理,正确的作出辅助线是解题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:解答题
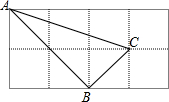 如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点上,这样的三角形叫做格点三角形,请画出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形可以画几个?
如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点上,这样的三角形叫做格点三角形,请画出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形可以画几个?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com