
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�ÿ��������60Ԫ��ÿ��������80Ԫ.���ۼ�Ϊÿ��60Ԫ�ǣ�ÿ���¿�����100�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������2��.��ÿ����Ʒ���ۼ�Ϊ![]() Ԫ��
Ԫ��![]() Ϊ����������ÿ���µ���������Ϊ
Ϊ����������ÿ���µ���������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ��
��![]() �ĺ�����ϵʽ��ֱ��д���Ա���
�ĺ�����ϵʽ��ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
��3����ÿ����Ʒ����Ϊ����Ԫʹ��ÿ���µ�����ǡΪ2250Ԫ��
���𰸡���1��![]()
![]() ����
����![]() ��
��![]() Ϊ����������2��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ����3��ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.
Ϊ����������2��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ����3��ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.
��������
��1�������ۼ�Ϊ60ʱ��ÿ������100�����ۼ�����Ӱ����������˸���60��x��80��ʽ��⣻
��2���ɣ�1������õĺ�������ʽ�������Ա���x�ķ�Χ����������ֵ��
��3����60��x��80����y=2250����ö���x��ֵ��
��1��![]()
![]() ����
����![]() ��
��![]() ������
������
��2��![]()
![]() ��
��
��![]() ���൱
���൱![]() ʱ��
ʱ��![]() �����ֵ2450.
�����ֵ2450.
��ÿ����Ʒ���ۼ۶�Ϊ75Ԫʱ��ÿ���¿ɻ���������������������2450Ԫ.
��3����![]() Ԫʱ��
Ԫʱ��![]() ��
��
��ã�![]() ��
��![]() ������
�����У�![]() ���������⣬��ȥ.
���������⣬��ȥ.
��˵�ÿ����Ʒ���ۼ�Ϊ65Ԫʱ��ÿ���µ�����ǡΪ2250Ԫ.


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
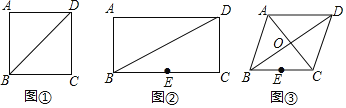
![]() ����ͼ
����ͼ![]() ��������ABCD�ĶԽ���BD����һ��P��ʹ
��������ABCD�ĶԽ���BD����һ��P��ʹ![]() ��С��
����
![]() ��ͼ
��ͼ![]() ����PΪ����ABCD�ĶԽ���BD��һ���㣬
����PΪ����ABCD�ĶԽ���BD��һ���㣬![]() ��
��![]() ����EΪBC�ߵ��е㣬����һ��P��ʹ
����EΪBC�ߵ��е㣬����һ��P��ʹ![]() ��С�����������Сֵ��
��С�����������Сֵ��
������
![]() ��ͼ
��ͼ![]() ����ʦ����һ��߳�Ϊ1000�����β�ժABCD��
����ʦ����һ��߳�Ϊ1000�����β�ժABCD��![]() �ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
�ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǰ�Բ
�ǰ�Բ![]() ��ֱ��������
��ֱ��������![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ��һ���㣬����
��һ���㣬����![]() ����
����![]() ��
��![]() ���ۣ���
���ۣ���![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ��ֱ��
��ֱ��![]() .
.

��1����![]() ʱ����֤��
ʱ����֤��![]() �ǰ�Բ
�ǰ�Բ![]() �����ߣ�
�����ߣ�
��2����![]() ������
������![]() �ϼ��������˶���ֱ��
�ϼ��������˶���ֱ��![]() �Ƿ���ٴ����Բ
�Ƿ���ٴ����Բ![]() ���У������У����
���У������У����![]() �Ķ������������У���˵������.
�Ķ������������У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����3��2����B��0��4����C��0��2����

��1��ƽ�ơ�ABC������A�Ķ�Ӧ��A1������Ϊ��0����4��������ƽ�ƺ��Ӧ�ġ�A1B1C1����д��B1��C1�����ꣻ
��2������ABC�Ե�CΪ��ת������ʱ����ת90�㣬������ת���Ӧ�ġ�A2B2C2����д��B2��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ĶԳ���Ϊ
�ĶԳ���Ϊ![]() ����
����![]() ���һ��������
���һ��������![]() ��
��![]() ֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���1��
֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��![]() Ϊ����ʵ��������4��
Ϊ����ʵ��������4��![]() ��5����
��5����![]()
![]()
![]() �Ǹ��������ϵĵ㣬��
�Ǹ��������ϵĵ㣬��![]() ��������ȷ���۵ĸ����ǣ� ��
��������ȷ���۵ĸ����ǣ� ��

A. 2B. 3C. 4D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ij����һ�ڼ����������Ϸ������������λ�ҳ��ֱ���Լ��ĺ��Ӳμ���Ϸ�����������Ѽҳ��ͺ���������������Ϸ��A��B��C�ֱ��ʾ��λ�ҳ������ǵĺ��ӷֱ��Ӧ����a��b��c��
��1���������˷ֱ����λ�ҳ�����λ�����и�ѡһ�˲μ���Ϸ��ǡ����A��a�ĸ����Ƕ��٣�ֱ��д���𰸣�
��2�����������ȴ���λ�ҳ�����ѡ����Ϊһ�飬�ٴӺ�������ѡ����Ϊһ�飬���˹�ͬ�μ���Ϸ��ǡ�������Լ�ͥ��Ա�ĸ����Ƕ��٣���������״ͼ���б���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
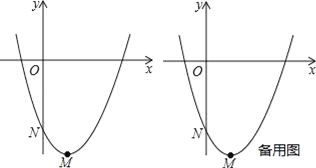
����Ŀ����֪������l��y=ax2+bx+c��a��b��c����Ϊ0���Ķ���ΪM����y��Ľ���ΪN�����dz���NΪ���㣬�Գ�����y���ҹ���M��������Ϊ������l�����������ߣ�ֱ��MNΪ������l������ֱ�ߣ�
��1����ͼ��������y=x2��2x��3�����������ߵĽ���ʽ���� ��������ֱ�ߵĽ���ʽ���� ����
��2����һ�������ߵ����������ߺ�����ֱ�߷ֱ���y=��2x2+1��y=��2x+1�������������ߵĽ���ʽ��
��3����ͼ���裨1���е�������y=x2��2x��3�Ķ���ΪM����y�ύ��ΪN������������ֱ��MN���Ƶ�N��ת����x��ƽ�У�����y������ƽ��1����λ��ֱ��n��P��ֱ��n�ϵĶ��㣬�Ƿ���ڵ�P��ʹ��POMΪֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
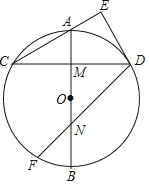
����Ŀ����ͼ��AB����O��ֱ����M��OA���е㣬��CD��AB�ڵ�M������D��DE��CA��CA���ӳ����ڵ�E��
(1)����AD�����OAD���� ���㣻
(2)��֤��DE����O���У�
(3)��F��![]() �ϣ���CDF��45�㣬DF��AB�ڵ�N����DE��3����FN�ij���
�ϣ���CDF��45�㣬DF��AB�ڵ�N����DE��3����FN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
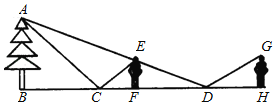
����Ŀ��С�����þ��Ӳ���һ�������ĸ߶ȣ�����������һ���ӣ����ܲ�����������֮��ľ��룬�������������þ��ӣ���ͼ��ʾ����һ�����Ѿ��ӷ���C�㣬����F��ʱ�����ھ����п�������A���ڶ��ΰѾ��ӷ���D�㣬����G�����ÿ�������A����֪С�����۾��������1.70m������CD��12m��CF��1.8m��DH��3.8m��������������ĸߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com