
(本题6分)如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.

(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决;小颖的想法:将△ABD沿AD所在的直线对折得到△ADF(如图2);小亮的想法:将△ABD绕点A顺时针旋转90°得到△ACG(如图3).请你选择其中的一种方法证明小敏的发现的是正确的.
见解析
【解析】
试题分析:(1)如图1,根据图形、已知条件推知∠BAD+∠MAE=∠DAM+∠EAC=45°,所以∠MAE=∠EAC,即AE平分∠MAC;(2)小颖的方法是应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△OCE中应用勾股定理而证明;小亮的方法是将△ABD绕点A逆时针旋转90°得到△ACG,根据旋转的性质用SAS得到△ACE≌△ACG,从而在Rt△CEG中应用勾股定理而证明.
试题解析:1)证明:如图1,∵∠BAC=90°,
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,即AE平分∠MAC;
(2)如图2,连接EF.

由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,
∵ AF=AC,∠FAE=∠CAE,AE=AE ,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2. (利用旋转的方法证明相应给分)
考点:1.全等三角形的判定与性质;2.勾股定理;3.等腰直角三角形.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片八年级上学期期中考试数学试卷(解析版) 题型:选择题
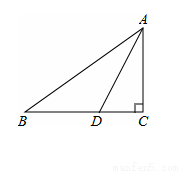
在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为__________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法正确的有几个( )
①经过三个点一定可以作圆;
②任意一个圆一定有内接三角形,并且只有一个内接三角形;
③任意一个三角形一定有一个外接圆并且只有一个外接圆;
④垂直于弦的直径必平分弦;
⑤经过不在同一直线上的四个点一定可以作圆.
A.3 B.2 C.1 D.0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片七年级上学期期中考试数学试卷(解析版) 题型:填空题
比较大小,用“<”“>”或“=”连接:
(1) 
(2)-3.14 -︱-π︱
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列代数式中,单项式共有( )
a, -2ab, 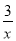 ,
,  ,
, 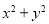 , -1,
, -1, 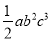
A.3个 B.4个 C.5个 D.6个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
三角板是我们常用的数学工具.下图是将其中一个三角板的直角顶点放在另一个等腰直角三角形斜边BC的中点D处转动,DE与AB交于点M,DF与AC交于点N(点M、N不与△ABC顶点重合),连接AD,若CN=2,DN= ,则线段AN的长为 。
,则线段AN的长为 。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题6分)钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船A的距离是多少.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列语句中正确的个数有( )
①角的对称轴是角的平分线.
②两个能全等的图形一定能关于某条直线对称.
③一个轴对称图形不一定只有一条对称轴.
④两个成轴对称的图形的对应点一定在对称轴的两侧.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com