考点:等腰三角形的性质
专题:
分析:(1)先由等边对等角的性质可设∠1=∠BCE=x°,∠2=∠ACD=y°,根据三角形内角和定理得出∠A=180°-2y°,∠B=180°-2x°,∠ACB+∠A+∠B=180°,则x+y=138,于是∠DCE=180°-(∠1+∠2)=180°-(x+y)=42°;
(2)由(1)可知∠DCE=180°-(∠1+∠2),再由∠A=180°-2∠2,∠B=180°-2∠1,得出∠1=90°-
∠B,∠2=90°-
∠A,将它们代入即可得出∠DCE=
(∠A+∠B),即可得到∠A,∠B与∠DCE之间的数量关系.
解答:解:(1)∵BE=BC,AD=AC,
∴设∠1=∠BCE=x°,∠2=∠ACD=y°,
∴∠A=180°-2∠2=180°-2y°,∠B=180°-2∠1=180°-2x°,
∵∠ACB+∠A+∠B=180°,
∴96+(180-2y)+(180-2x)=180,
∴x+y=138,
∴∠DCE=180°-(∠1+∠2)=180°-(x+y)=42°;
(2)由(1)可知∠DCE=180°-(∠1+∠2),
∵∠A=180°-2∠2,∠B=180°-2∠1,
∴∠1=90°-
∠B,∠2=90°-
∠A,
∴∠DCE=180°-(90°-
∠B+90°-
∠A)
=
(∠A+∠B),
∴∠A+∠B=2∠DCE.
点评:本题考查了等腰三角形的性质,三角形内角和定理,难度适中.

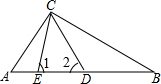 如图,在△ABC中,AD=AC,BE=BC.
如图,在△ABC中,AD=AC,BE=BC.
