
【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

【答案】(1)y=![]() x2+x﹣4;(2)点D的坐标为(0,2)或(0,﹣2)或(0,8)或(0,﹣8);(3)P点的横坐标为﹣2或
x2+x﹣4;(2)点D的坐标为(0,2)或(0,﹣2)或(0,8)或(0,﹣8);(3)P点的横坐标为﹣2或![]() .
.
【解析】分析:![]() 根据对称轴坐标公式可求二次函数图象的对称轴;当x=0时,y=4,可求点C的坐标为(0,4),,根据三角形面积公式可求
根据对称轴坐标公式可求二次函数图象的对称轴;当x=0时,y=4,可求点C的坐标为(0,4),,根据三角形面积公式可求![]() 进一步得到A点和B点的坐标分别为(4,0),(2,0).待定系数法可求二次函数的解析式.
进一步得到A点和B点的坐标分别为(4,0),(2,0).待定系数法可求二次函数的解析式.
![]()
![]() 则分
则分![]() 和
和![]() 两种情况讨论即可.
两种情况讨论即可.
![]() 过D作
过D作![]() 轴于F,分两种情况:①当点P在直线AD的下方时,②当点P在直线AD的上方时.分别求解.
轴于F,分两种情况:①当点P在直线AD的下方时,②当点P在直线AD的上方时.分别求解.
详解:(1)该二次函数的对称轴是:直线![]()
当x=0时,y=4,
∴点C的坐标为(0,4),
∴![]()
连接![]()
∵![]()
![]()
又∵点A,B关于直线x=1对称,
∴A点和B点的坐标分别为(4,0),(2,0).
∴4a+4a4=0,解得![]()
∴所求二次函数的解析式为![]()
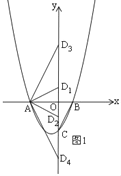
(2)如图1,∵![]()
且![]()
![]()
分两种情况:
①当![]() 时,
时,![]()
∴![]()
即![]() 或
或![]()
②当![]() 时,
时,![]()
∴![]()
即![]() 或
或![]()
综上所述,点D的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
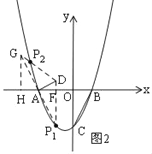
(3)如图2,过D作![]() 轴于F,分两种情况:
轴于F,分两种情况:
①当点P在直线AD的下方时,如图所示:
由(1)得点A(4,0),点D(2,1),
∴DF=1,AF=2.
在Rt△ADF中,![]() 得
得![]()
延长DF与抛物线交于点![]() ,则
,则![]() 点为所求,
点为所求,
∴点![]() 的坐标为(2,4).
的坐标为(2,4).
②当点P在直线AD的上方时,延长P1A至点G使得AG=AP1,连接DG,作GH⊥x轴于点H,如图所示.
可证△GHA≌△P1FA.
∴HA=AF,GH=P1F,GA=P1A.
又∵A(4,0),P1(2,4),
∴点G的坐标是(6,4).
易得DG的解析式为:![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
设DG与抛物线的交点为P2,则P2点为所求,设![]()
代入DG的解析式中,![]()
解得![]()
∵P2 点在第二象限,
∴P2点的横坐标为![]() (舍正)
(舍正)
综上,P点的横坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】我们在“堆石子”游戏中发现:像图(1)中的![]() 这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的
这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的![]() 这些数据能够表示成三角形,可将其称为三角形数.
这些数据能够表示成三角形,可将其称为三角形数.

(1)第![]() 个正方形数是 ;第
个正方形数是 ;第![]() 个正方形数是 ;
个正方形数是 ;
(2)第![]() 个三角形数是 ;第
个三角形数是 ;第![]() 个三角形数是 ;
个三角形数是 ;
(3)若将一堆小石子按一定规律摆成下列图形,请求出第![]() 个图形中“●”的个数.
个图形中“●”的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且![]() ,联结CM、DN.
,联结CM、DN.
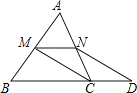
(1)求证:四边形MCDN是平行四边形;
(2)若三角形AMN的面积等于5,求梯形MBDN的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度通常有两种表示方法:华氏度(单位:![]() )与摄氏度(单位:
)与摄氏度(单位:![]() ).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
摄氏度数x( | … | 0 | … | 35 | … | 100 | … |
华氏度数y( | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是![]()
![]() ,求与之对应的华氏度数.
,求与之对应的华氏度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
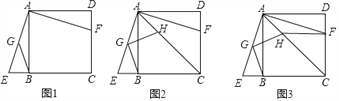
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com