
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
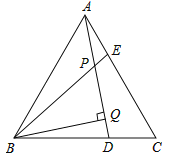
A.7B.8C.9D.10
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
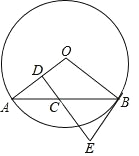
【题目】如图,AB 是⊙O 的一条弦,C 是 AB 的中点,过点 C 作直线垂直于OA 于点 D,交过点 B 的⊙O 的切线于点 E.
(1)求证:BE=CE;
(2)若⊙O 的半径长为 8,AB=12,求 BE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,﹣1),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO.
,0)与点B(0,﹣1),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)请直接写出⊙M的直径,并求证BD平分∠ABO;
(2)在线段BD的延长线上寻找一点E,使得直线AE恰好与⊙M相切,求此时点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.

(1)若点![]() 是
是![]() 轴上的一动点,连接
轴上的一动点,连接![]() 、
、![]() ,当
,当![]() 的值最小时,求出点
的值最小时,求出点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
(2)如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,再将
,再将![]() 绕点
绕点![]() 作顺时针方向旋转,旋转角度为
作顺时针方向旋转,旋转角度为![]() ,记旋转中的三角形为
,记旋转中的三角形为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,当
,当![]() 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com