
ΓΨΧβΡΩΓΩΡ≥ –œ÷‘Ύ”–ΝΫ÷÷”ΟΒγ ’Ζ―ΖΫΖ®ΘΚ
Ζ÷ ±Βγ±μ | Τ’Ά®Βγ±μ | |
Ζε ±Θ®8:00ΓΪ21:00Θ© | Ι» ±Θ®21:00ΒΫ¥Έ»’8:00Θ© | |
ΒγΦέ0.55‘Σ/«ßΆΏΓΛ ± | ΒγΦέ0.35‘Σ/«ßΆΏΓΛ ± | ΒγΦέ0.52‘Σ/«ßΆΏΓΛ ± |
–ΓΟςΦ“Υυ‘ΎΒΡ–Γ«χ”ΟΒΡΒγ±μΕΦΜΜ≥…ΝΥΖ÷ ±Βγ±μ.
ΫβΨωΈ ΧβΘΚ
Θ®1Θ©–ΓΟςΦ“ΆΞΡ≥‘¬”ΟΒγΉήΝΩΈΣ![]() «ßΆΏΓΛ ±Θ®
«ßΆΏΓΛ ±Θ®![]() ΈΣ≥Θ ΐΘ©ΘΜΙ» ±”ΟΒγ
ΈΣ≥Θ ΐΘ©ΘΜΙ» ±”ΟΒγ![]() «ßΆΏΓΛ ±Θ§Ζε ±”ΟΒγ
«ßΆΏΓΛ ±Θ§Ζε ±”ΟΒγ![]() «ßΆΏΓΛ ±Θ§Ζ÷ ±ΦΤΦέ ±ΉήΦέΈΣ
«ßΆΏΓΛ ±Θ§Ζ÷ ±ΦΤΦέ ±ΉήΦέΈΣ![]() ‘ΣΘ§Τ’Ά®ΦΤΦέ ±ΉήΦέΈΣ
‘ΣΘ§Τ’Ά®ΦΤΦέ ±ΉήΦέΈΣ![]() ‘ΣΘ§«σ
‘ΣΘ§«σ![]() Θ§
Θ§![]() ”κ”ΟΒγΝΩΒΡΚ· ΐΙΊœΒ Ϋ.
”κ”ΟΒγΝΩΒΡΚ· ΐΙΊœΒ Ϋ.
Θ®2Θ©–ΓΟςΦ“ΆΞ Ι”ΟΖ÷ ±Βγ±μ «≤Μ «“ΜΕ®±»Τ’Ά®Βγ±μΚœΥψΡΊΘΩ
Θ®3Θ©œ¬±μ «¬Ζπ©Φ“ΉνΫϋΝΫΗω‘¬”ΟΒγΒΡ ’ΨίΘΚ
Ι» ±”ΟΒγΘ®«ßΆΏΓΛ ±Θ© | Ζε ±”ΟΒγΘ®«ßΆΏΓΛ ±Θ© |
181 | 239 |
ΗυΨί…œ±μΘ§«κΈ ”ΟΖ÷ ±Βγ±μ «ΖώΚœΥψΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©y1=0.35x+0.55Θ®a-xΘ©Θ§y2=0.52aΘΜΘ®2Θ©Β±xΘΨ![]() ±Θ§ Ι”ΟΖ÷ ±Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜΒ±x=
±Θ§ Ι”ΟΖ÷ ±Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜΒ±x=![]() ±Θ§ΝΫ÷÷Βγ±μΖ―”ΟœύΆ§ΘΜΒ±xΘΦ
±Θ§ΝΫ÷÷Βγ±μΖ―”ΟœύΆ§ΘΜΒ±xΘΦ![]() ±Θ§ Ι”ΟΤ’Ά®Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜΘ®3Θ©”ΟΖ÷ ±Βγ±μΗϋΚœΥψ.
±Θ§ Ι”ΟΤ’Ά®Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜΘ®3Θ©”ΟΖ÷ ±Βγ±μΗϋΚœΥψ.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβ“βΫβ¥πΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΝ–≤ΜΒ» ΫΫβ¥πΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΘ®1Θ©ΒΡΫα¬έΫβ¥πΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΗυΨίΧβ“βΒΟΘΚy1=0.35x+0.55Θ®a-xΘ©Θ§y2=0.52aΘΜ
Θ®2Θ©–ΓΟςΦ“ΆΞ Ι”ΟΖ÷ ±Βγ±μ≤Μ“ΜΕ®±»Τ’Ά®Βγ±μΚœΥψΘ°
Β±y1ΘΦy2Θ§Φ¥0.35x+0.55Θ®a-xΘ©ΘΦ0.52aΘ§ΫβΒΟxΘΨ![]() Θ§
Θ§
Φ¥xΘΨ![]() ±Θ§ Ι”ΟΖ÷ ±Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜ
±Θ§ Ι”ΟΖ÷ ±Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜ
Β±y1=y2Θ§Φ¥0.35x+0.55Θ®a-xΘ©=0.52aΘ§ΫβΒΟx=![]() Θ§
Θ§
Φ¥x=![]() ±Θ§ΝΫ÷÷Βγ±μΖ―”ΟœύΆ§ΘΜ
±Θ§ΝΫ÷÷Βγ±μΖ―”ΟœύΆ§ΘΜ
Β±y1ΘΨy2Θ§Φ¥0.35x+0.55Θ®a-xΘ©ΘΨ0.52aΘ§ΫβΒΟxΘΦ![]() Θ§
Θ§
Φ¥xΘΦ![]() ±Θ§ Ι”ΟΤ’Ά®Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜ
±Θ§ Ι”ΟΤ’Ά®Βγ±μ±»Τ’Ά®Βγ±μΚœΥψΘΜ
Θ®3Θ©”ΟΖ÷ ±Βγ±μΒΡΖ―”ΟΈΣΘΚ0.35ΓΝ181+0.55ΓΝ239=194.8Θ®‘ΣΘ©ΘΜ
Ι”ΟΤ’Ά®Βγ±μΒΡΖ―”ΟΈΣΘΚ0.52ΓΝΘ®181+239Θ©=218.4Θ®‘ΣΘ©Θ°
Υυ“‘”ΟΖ÷ ±Βγ±μΗϋΚœΥψΘ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
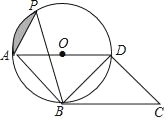
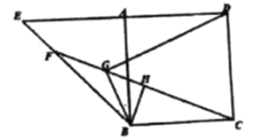
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςPABΡΎΫ””ΎΓ―OΘ§ABCDΒΡ±ΏAD «Γ―OΒΡ÷±ΨΕΘ§«“ΓœCΘΫΓœAPBΘ§Ν§Ϋ”BDΘ°
Θ®1Θ©«σ÷ΛΘΚBC «Γ―OΒΡ«–œΏΘ°
Θ®2Θ©»τBCΘΫ2Θ§ΓœPBDΘΫ60ΓψΘ§«σ![]() ”κœ“APΈß≥…ΒΡ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
”κœ“APΈß≥…ΒΡ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
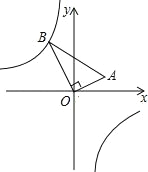
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςAOB÷–Θ§ΓœAOBΘΫ90ΓψΘ§ΒψAΒΡΉχ±ξΈΣΘ®4Θ§2Θ©Θ§BOΘΫ4![]() Θ§Ζ¥±»άΐΚ· ΐyΘΫ
Θ§Ζ¥±»άΐΚ· ΐyΘΫ![]() ΒΡΆΦœσΨ≠ΙΐΒψBΘ§‘ρkΒΡ÷ΒΈΣ_____Θ°
ΒΡΆΦœσΨ≠ΙΐΒψBΘ§‘ρkΒΡ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
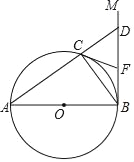
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§÷±œΏBMΓΆAB”ΎΒψBΘ§ΒψC‘ΎΓ―O…œΘ§Ζ÷±πΝ§Ϋ”BCΘ§ACΘ§«“ACΒΡ―”≥ΛœΏΫΜBM”ΎΒψDΘ§CFΈΣΓ―OΒΡ«–œΏΫΜBM”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚCFΘΫDFΘΜ
Θ®2Θ©Ν§Ϋ”OFΘ§»τABΘΫ10Θ§BCΘΫ6Θ§«σœΏΕΈOFΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§«“
Θ§«“![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ≥ΛΈΣΘ® Θ©
ΒΡ≥ΛΈΣΘ® Θ©
A.7B.8C.9D.10
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
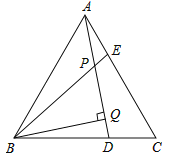
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ΈΣ
ΈΣ![]() ―”≥ΛœΏ…œ“ΜΒψ«“
―”≥ΛœΏ…œ“ΜΒψ«“![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§‘Ύ
Θ§‘Ύ![]() …œΫΊ»Γ
…œΫΊ»Γ![]() Θ§ Ι
Θ§ Ι![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]() Θ§Ζ÷±πΫΜ
Θ§Ζ÷±πΫΜ![]() ”ΎΒψ
”ΎΒψ![]() ΓΔ
ΓΔ![]() .Ν§Ϋ”
.Ν§Ϋ”![]() .
.
Θ®1Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗχΕ®ΙΊ”Ύ![]() ΒΡΕΰ¥ΈΚ· ΐ
ΒΡΕΰ¥ΈΚ· ΐ![]() Θ§
Θ§
―ß…ζΦΉΘΚΒ±![]() ±Θ§≈ΉΈοœΏ”κ
±Θ§≈ΉΈοœΏ”κ ![]() ÷α÷Μ”–“ΜΗωΫΜΒψΘ§“ρ¥ΥΒ±≈ΉΈοœΏ”κ
÷α÷Μ”–“ΜΗωΫΜΒψΘ§“ρ¥ΥΒ±≈ΉΈοœΏ”κ![]() ÷α÷Μ”–“ΜΗωΫΜΒψ ±Θ§
÷α÷Μ”–“ΜΗωΫΜΒψ ±Θ§![]() ΒΡ÷ΒΈΣ3ΘΜ
ΒΡ÷ΒΈΣ3ΘΜ
―ß…ζ““ΘΚ»γΙϊ≈ΉΈοœΏ‘Ύ![]() ÷α…œΖΫΘ§Ρ«Ο¥ΗΟ≈ΉΈοœΏΒΡΉνΒΆΒψ“ΜΕ®‘ΎΒΎΕΰœσœόΘΜ
÷α…œΖΫΘ§Ρ«Ο¥ΗΟ≈ΉΈοœΏΒΡΉνΒΆΒψ“ΜΕ®‘ΎΒΎΕΰœσœόΘΜ
«κ≈–Εœ―ß…ζΦΉΓΔ““ΒΡΙέΒψ «Ζώ’ΐ»ΖΘ§≤ΔΥΒΟςΡψΒΡάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΟςΆΕΉ œζ έ“Μ÷÷ΫχΦέΈΣΟΩΦΰ20‘ΣΒΡΜΛ―έΧ®ΒΤΘ°œζ έΙΐ≥Χ÷–ΖΔœ÷Θ§ΟΩ‘¬œζ έΝΩyΘ®ΦΰΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΒΡΙΊœΒΩ…ΫϋΥΤΒΡΩ¥Ής“Μ¥ΈΚ· ΐΘΚy=©¹10x+500Θ§‘Ύœζ έΙΐ≥Χ÷–œζ έΒΞΦέ≤ΜΒΆ”Ύ≥…±ΨΦέΘ§ΕχΟΩΦΰΒΡάϊ»σ≤ΜΗΏ”Ύ≥…±ΨΦέΒΡ60%Θ°
Θ®1Θ©…η–ΓΟςΟΩ‘¬ΜώΒΟάϊ»σΈΣwΘ®‘ΣΘ©Θ§«σΟΩ‘¬ΜώΒΟάϊ»σwΘ®‘ΣΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ»ΖΕ®Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®2Θ©Β±œζ έΒΞΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§ΟΩ‘¬Ω…ΜώΒΟΉν¥σάϊ»σΘΩΟΩ‘¬ΒΡΉν¥σάϊ»σ «Εύ…ΌΘΩ
Θ®3Θ©»γΙϊ–ΓΟςœκ“ΣΟΩ‘¬ΜώΒΟΒΡάϊ»σ≤ΜΒΆ”Ύ2000‘ΣΘ§Ρ«Ο¥–ΓΟςΟΩ‘¬ΒΡ≥…±ΨΉν…Ό–η“ΣΕύ…Ό‘ΣΘΩΘ®≥…±Ψ=ΫχΦέΓΝœζ έΝΩΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
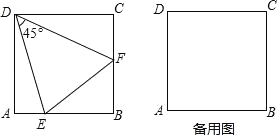
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–Έ ABCD ÷–Θ§E ΈΣ÷±œΏ AB …œΒΡΕ·ΒψΘ®≤Μ”κ AΓΔB ÷ΊΚœΘ©Θ§Ής…δœΏ DE ≤Δ»ΤΒψ D Ρφ ±’κ–ΐΉΣ 45ΓψΘ§ΫΜ÷±œΏ BC ”ΎΒψ FΘ§Ν§Ϋ” EFΘ°
ΧΫΨΩΘΚΒ±Βψ E ‘Ύ±Ώ AB …œΘ§«σ÷ΛΘΚEFΘΫAE+CFΘ°
”Π”ΟΘΚ(1)Β±Βψ E ‘Ύ±Ώ AB …œΘ§«“ ADΘΫ2 ±Θ§«σΓςBEF ΒΡ÷ή≥ΛΘΜ
(2)Β±Βψ E ‘Ύ BA ―”≥ΛœΏ…œ ±Θ§≈–Εœ EFΘ§AEΘ§CF »ΐ’ΏΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com