
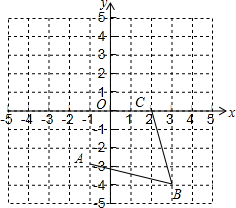
 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,分析 (1)设D(x,y),再由菱形的对角线互相垂直平分即可得出结论;
(2)先根据勾股定理求出菱形的边长,进而可得出其周长;利用正方形的面积减去四个顶点上三角形的面积即可得出菱形的面积;
(3)过点C作CE⊥AB于点E,先利用待定系数法求出直线AB的解析式,再根据CE⊥AB求出直线CE的解析式,故可得出E点坐标,利用两点间的距离公式求出CE的长,由锐角三角函数的定义即可得出结论.
解答 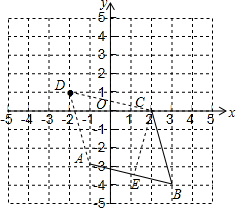 解:(1)设D(x,y),
解:(1)设D(x,y),
∵A(-1,-3),B(3,-4),C(2,0),
∴$\frac{-1+2}{2}$=$\frac{3+x}{2}$,$\frac{-3}{2}$=$\frac{-4+y}{2}$,
解得x=-2,y=1,
∴点D的坐标(-2,1).
故答案为:(-2,1);
(2)∵AB=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴菱形ABCD的周长为$4\sqrt{17}$;
菱形ABCD的面积=5×5-4×$\frac{1}{2}$×1×4-2=25-8-2=15.
故答案为:4$\sqrt{17}$,15;
(3)过点C作CE⊥AB于点E,设直线AB的解析式为y=kx+b(k≠0),
∵A(-1,-3),B(3,-4),
∴$\left\{\begin{array}{l}-k+b=-3\\ 3k+b=-4\end{array}\right.$,
解得$\left\{\begin{array}{l}b=-\frac{13}{4}\\ k=-\frac{1}{4}\end{array}\right.$.
∴直线AB的解析式为y=-$\frac{1}{4}$x-$\frac{13}{4}$.
设直线CE的解析式为y=4x+c(a≠0),
∵C(2,0),
∴8+c=0,解得c=-8,
∵设直线CE的解析式为y=4x-8,
∴$\left\{\begin{array}{l}y=-\frac{1}{4}x-\frac{13}{4}\\ y=4x-8\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{19}{17}\\ y=-\frac{60}{17}\end{array}\right.$,
∴E($\frac{19}{17}$,-$\frac{60}{17}$),
∴CE=$\sqrt{(2-\frac{19}{17})^{2}+(\frac{60}{17})^{2}}$=$\frac{15\sqrt{17}}{17}$,
∴sin∠CBA=$\frac{CE}{BC}$=$\frac{\frac{15\sqrt{17}}{17}}{\sqrt{17}}$=$\frac{15}{17}$.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质及菱形的性质是解答此题的关键.


科目:初中数学 来源: 题型:选择题
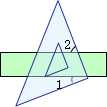 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=25°,那么∠2等于( )| A. | 25° | B. | 65° | ||
| C. | 75° | D. | 以上结果均不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
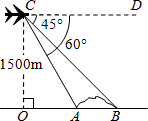 如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).
如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
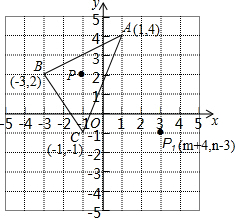 如图,三角形ABC中任一点P(m,n)经平移后对应点为P1(m+4,n-3),将三角形ABC作同样的平移得到三角形A1B1C1.
如图,三角形ABC中任一点P(m,n)经平移后对应点为P1(m+4,n-3),将三角形ABC作同样的平移得到三角形A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
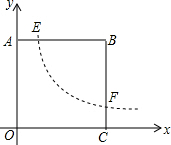 如图,正方形ABCD,AB、BC与反比例函数(y=$\frac{k}{x}$x>0)的图象交于E、F两点,且OE2-BF2=4,则k=2.
如图,正方形ABCD,AB、BC与反比例函数(y=$\frac{k}{x}$x>0)的图象交于E、F两点,且OE2-BF2=4,则k=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com