
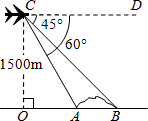
 如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).
如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
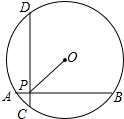 如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
如图,在半径为10的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{x+1}$ | C. | $\frac{2}{x+1}$ | D. | $\frac{2}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
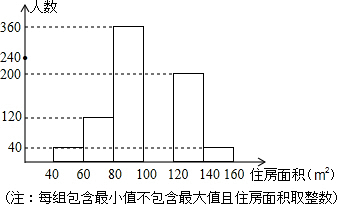 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 3.2 | 3.8 | 5.0 | 7.0 | 12.0 |
| 被调查的消费者数(人) | 200 | 500 | 200 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
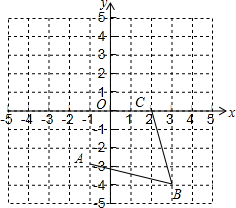 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
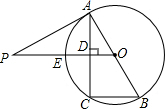 如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com