
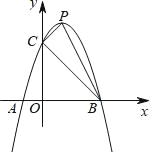
【题目】如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.
(1)求抛物线的解析式.
(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.
(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)①Q(2,3);②Q2(![]() ,
, ![]() ),Q3(
),Q3(![]() ,
,![]() );(3)存在点M,N使四边形MNED为正方形,MN=9
);(3)存在点M,N使四边形MNED为正方形,MN=9![]() 或
或![]() .理由见解析.
.理由见解析.
【解析】
(1)设出抛物线顶点坐标,把C坐标代入求出即可;
(2)由△BCQ与△BCP的面积相等,得到PQ与BC平行,①过P作作PQ∥BC,交抛物线于点Q,如图1所示;②设G(1,2),可得PG=GH=2,过H作直线Q2Q3∥BC,交x轴于点H,分别求出Q的坐标即可;
(3)存在点M,N使四边形MNED为正方形,如图2所示,过M作MF∥y轴,过N作NF∥x轴,过N作NH∥y轴,则有△MNF与△NEH都为等腰直角三角形,设M(x1,y1),N(x2,y2),设直线![]() 解析式为y=-x+b,与二次函数解析式联立,消去y得到关于x的一元二次方程,利用根与系数关系表示出NF2,由△MNF为等腰直角三角形,得到MN2=2NF2,若四边形MNED为正方形,得到NE2=MN2,求出b的值,进而确定出MN的长,即为正方形边长.
解析式为y=-x+b,与二次函数解析式联立,消去y得到关于x的一元二次方程,利用根与系数关系表示出NF2,由△MNF为等腰直角三角形,得到MN2=2NF2,若四边形MNED为正方形,得到NE2=MN2,求出b的值,进而确定出MN的长,即为正方形边长.
(1)设y=a(x﹣1)2+4(a≠0),
把C(0,3)代入抛物线解析式得:a+4=3,即a=﹣1,
则抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)由B(3,0),C(0,3),得到直线BC解析式为y=﹣x+3,
∵S△OBC=S△QBC,
∴PQ∥BC,
①过P作PQ∥BC,交抛物线于点Q,如图1所示,
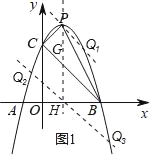
∵P(1,4),∴直线PQ解析式为y=﹣x+5,
联立得:![]() ,
,
解得:![]() 或
或![]() ,即Q(2,3);
,即Q(2,3);
②设G(1,2),∴PG=GH=2,
过H作直线Q2Q3∥BC,交x轴于点H,则直线Q2Q3解析式为y=﹣x+1,
联立得:![]() ,
,
解得: 或
或 ,
,
∴Q2(![]() ,
,![]() ),Q3(
),Q3(![]() ,
,![]() );
);
(3)存在点M,N使四边形MNED为正方形,
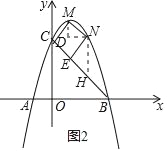
如图2所示,过M作MF∥y轴,过N作NF∥x轴,过N作NH∥y轴,则有△MNF与△NEH都为等腰直角三角形,
设M(x1,y1),N(x2,y2),设直线MN解析式为y=﹣x+b,
联立得:![]() ,
,
消去y得:x2﹣3x+b﹣3=0,
∴NF2=|x1﹣x2|2=(x1+x2)2﹣4x1x2=21﹣4b,
∵△MNF为等腰直角三角形,
∴MN2=2NF2=42﹣8b,
∵NH2=(b﹣3)2,∴NF2=![]() (b﹣3)2,
(b﹣3)2,
若四边形MNED为正方形,则有NE2=MN2,
∴42﹣8b=![]() (b2﹣6b+9),
(b2﹣6b+9),
整理得:b2+10b﹣75=0,
解得:b=﹣15或b=5,
∵正方形边长为MN=![]() ,
,
∴MN=9![]() 或
或![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
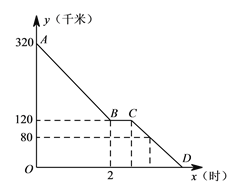
【题目】上周六上午![]() 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离![]() (千米)与他们路途所用的时间
(千米)与他们路途所用的时间![]() (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:
(1)求直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)已知小颖一家出服务区后,行驶![]() 分钟时,距姥姥家还有
分钟时,距姥姥家还有![]() 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?
查看答案和解析>>
科目:初中数学 来源: 题型:
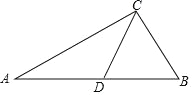
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
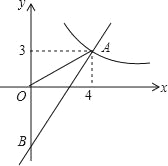
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
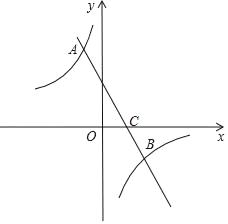
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com