
【题目】在平面直角坐标系中,直线AB分别交x轴,y轴于A(a,0),B(0,b),且满足a2+b2+4a﹣8b+20=0.

(1)求a,b的值;
(2)点P在直线AB的右侧;且∠APB=45°,
①若点P在x轴上(图1),则点P的坐标为 ;
②若△ABP为直角三角形,求P点的坐标.
【答案】(1)a=﹣2,b=4;(2)①(4,0);②P点坐标为(4,2),(2,﹣2).
【解析】
(1)利用非负数的性质解决问题即可.
(2)①根据等腰直角三角形的性质即可解决问题.
②分两种情形:如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.分别利用全等三角形的性质解决问题即可.
(1)∵a2+4a+4+b2﹣8b+16=0
∴(a+2)2+(b﹣4)2=0
∴a=﹣2,b=4.
(2)①如图1中,
∵∠APB=45°,∠POB=90°,
∴OP=OB=4,
∴P(4,0).
故答案为(4,0).
②∵a=﹣2,b=4
∴OA=2OB=4
又∵△ABP为直角三角形,∠APB=45°
∴只有两种情况,∠ABP=90°或∠BAP=90°
①如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.
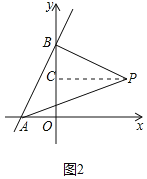
∴∠PCB=∠BOA=90°,
又∵∠APB=45°,
∴∠BAP=∠APB=45°,
∴BA=BP,
又∵∠ABO+∠OBP=∠OBP+∠BPC=90°,
∴∠ABO=∠BPC,
∴△ABO≌△BPC(AAS),
∴PC=OB=4,BC=OA=2,
∴OC=OB﹣BC=4﹣2=2,
∴P(4,2).
②如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.
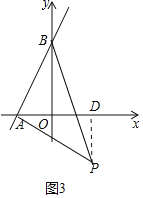
∴∠PDA=∠AOB=90°,
又∵∠APB=45°,
∴∠ABP=∠APB=45°,
∴AP=AB,
又∵∠BAD+∠DAP=90°,
∠DPA+∠DAP=90°,
∴∠BAD=∠DPA,
∴△BAO≌△APP(AAS),
∴PD=OA=2,AD=OB=4,
∴OD=AD﹣0A=4﹣2=2,
∴P(2,﹣2).
综上述,P点坐标为(4,2),(2,﹣2).


科目:初中数学 来源: 题型:
【题目】已知y是关于x的一次函数,下表列出了这个函数部分的对应值:

(1)求这个一次函数的表达式.
(2)求m,n的值.
(3)已知点![]() 和点
和点![]() 在该一次函数图象上,设
在该一次函数图象上,设![]() ,判断正比例函数
,判断正比例函数![]() 的图象是否有可能经过第一象限,并说明理由.
的图象是否有可能经过第一象限,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC 中,AB=AC,点 D 在 AB 边上,点 E 在 AC 的延长线上,且 CE=BD, 连接 DE 交 BC 于点 F.

⑴求证:EF=DF;
⑵如图2,过点 D 作 DG⊥BC,垂足为 G,求证:BC=2FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
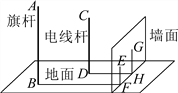
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,请在图中画出△AMN,写出画图过程并直接写出∠MAN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
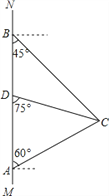
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,弦
的弦,弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 的直线与
的直线与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 当点
当点![]() 在劣弧
在劣弧![]() 上运动时,其他条件不变,若
上运动时,其他条件不变,若![]() .求证:点
.求证:点![]() 是
是![]() 的中点;
的中点;
![]() 在满足
在满足![]() 的条件下,
的条件下,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com