
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.
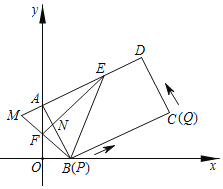
【答案】(1)E(m,m+n);(2)详见解析;(3)存在,![]() cm/s或2cm/s.
cm/s或2cm/s.
【解析】
(1)过E作EG⊥AO于G.证明△EGA≌△AOB(AAS)即可解决问题.
(2)想办法证明△EAN≌△BAM(ASA)即可解决问题.
(3)分两种情形分别求解即可解决问题.
解:(1)过E作EG⊥AO于G.
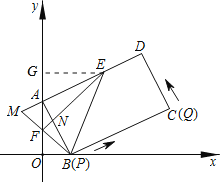
∵∠EGA=∠EAB=∠AOB=90°,
∴∠EAG+∠AEG=90°,∠EAG+∠BAO=90°,
∴∠BAO=∠AEG,
∵AE=AB,
∴△EGA≌△AOB(AAS),
∴EG=OA=m,AG=OB=n
∴E(m,m+n).
(2)∵OB=OF,∠BOF=90°,
∴∠OFB=∠OBF=45°,
∵△EGA≌△AOB,
∴AG=OB=OF,
∴OA=FG=EG,
∴∠GFE=45°,
∴∠EFB=90°,
∴∠NAE=∠NFB=90°,∵∠ANE=∠FNB,
∴∠AEN=∠ABM,
∵∠EAN=∠BAM=90°,EA=BA,
∴△EAN≌△BAM(ASA),
∴AN=AM.
(3)如图,∵△ABP与△PCQ全等,∠ABP=∠PCQ=90°

∴有两种情形:①当AB=CD,PB=CP时,t=![]() =5(s),
=5(s),
∴v=![]() (cm/s),
(cm/s),
②当AB=PC,CQ=PB时,
PB=20﹣12=8,
∴t=![]() =4(s),
=4(s),
∴v=![]() =
=![]() =2(cm/s).
=2(cm/s).
综上可知,当![]() cm/s或2 cm/s时,△ABP与△PQC全等.
cm/s或2 cm/s时,△ABP与△PQC全等.


科目:初中数学 来源: 题型:
【题目】近日,在公安部交通管理局部署下,全国各地交警都在大力开展|一盔一带安全守护行动,为了解市民对骑电动车戴头盔的赞同情况,某课题小组随机调查了部分市民,并根据调查结果绘制了尚不完整的统计图.
根据以上统计图回答一下问题:
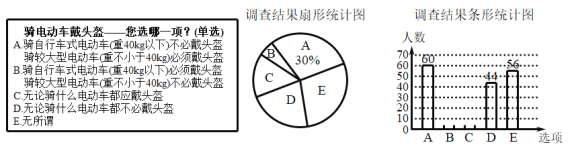
(1)这次调查的市民共_______人;
(2)若选择![]() 的人数是选择
的人数是选择![]() 的人数的3倍,则扇形统计图中,扇形
的人数的3倍,则扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)补全条形统计图;
(4)若该市约有80万人,请估计安全意识淡薄(选择D或E)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数![]() (
(![]() 是常数)时,甲发现当
是常数)时,甲发现当![]() 时,函数有最小值;乙发现
时,函数有最小值;乙发现![]() 是方程
是方程![]() 的一个根;丙发现函数的最小值为3;丁发现当
的一个根;丙发现函数的最小值为3;丁发现当![]() 时,
时,![]() ,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
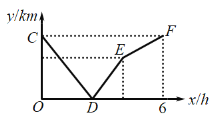
【题目】A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线![]() 所示.其中点C的坐标是
所示.其中点C的坐标是![]() ,点D的坐标是
,点D的坐标是![]() ,则点E的坐标是__________.
,则点E的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
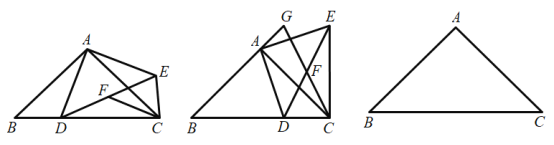
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.
(1)求证:![]() ;
;
(2)如图2所示,在点D运动的过程中,当![]() 时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
(3)在点D运动的过程中,在线段AD上存在一点P,使![]() 的值最小.当
的值最小.当![]() 的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.
的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
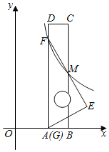
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数![]() (x
(x![]() 0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=
0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=![]() ,则k=____.
,则k=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
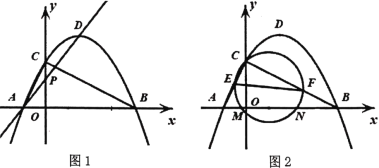
【题目】如图![]() ,二次函数
,二次函数![]() (
(![]() 、
、![]() 为参数,其中
为参数,其中![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)若![]() ,求
,求![]() 的值(结果用含
的值(结果用含![]() 的式子表示);
的式子表示);
(2)若![]() 是等腰三角形,直线
是等腰三角形,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() .求抛物线的解析式;
.求抛物线的解析式;
(3)如图![]() ,已知
,已知![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,并交
,并交![]() 轴于
轴于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com