
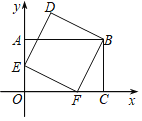
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
【答案】C
【解析】
过D作DH⊥y轴于H,根据矩形和正方形的性质得到AO=BC,DE=EF=BF,∠AOC=∠DEF=∠BFE=∠BCF=90°,根据全等三角形的性质即可得到结论.
过D作DH⊥y轴于H,
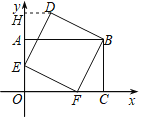
∵四边形AOCB是矩形,四边形BDEF是正方形,
∴AO=BC,DE=EF=BF,
∠AOC=∠DEF=∠BFE=∠BCF=90°,
∴∠OEF+∠EFO=∠BFC+∠EFO=90°,
∴∠OEF=∠BFO,
∴△EOF≌△FCB(ASA),
∴BC=OF,OE=CF,
∴AO=OF,
∵E是OA的中点,
∴OE=![]() OA=
OA=![]() OF=CF,
OF=CF,
∵点C的坐标为(3,0),
∴OC=3,
∴OF=OA=2,AE=OE=CF=1,
同理△DHE≌△EOF(ASA),
∴DH=OE=1,HE=OF=2,
∴OH=2,
∴点D的坐标为(1,3),
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线![]() 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线![]() 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线![]() 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果点![]() 、点
、点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 、
、![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 、
、![]() 的“极好菱形”.如图为点
的“极好菱形”.如图为点![]() 、
、![]() 的“极好菱形”的一个示意图.已知点
的“极好菱形”的一个示意图.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
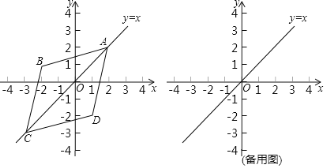
(1)点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“极好菱形”的顶点的是 .
的“极好菱形”的顶点的是 .
(2)若点![]() 、
、![]() 的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标.
的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标.
(3)如果四边形![]() 是点
是点![]() 、
、![]() 的“极好菱形”.
的“极好菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
②当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
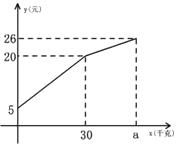
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点![]() 关于原点的对称点为
关于原点的对称点为![]() ,以
,以![]() 为边作等边
为边作等边![]() ,则称点
,则称点![]() 为
为![]() 的“等边对称点”;
的“等边对称点”;
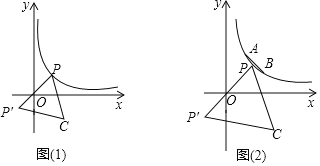
(1)若![]() ,求点
,求点![]() 的“等边对称点”的坐标;
的“等边对称点”的坐标;
(2)若![]() 点是双曲线
点是双曲线![]() 上动点,当点
上动点,当点![]() 的“等边对称点”点
的“等边对称点”点![]() 在第四象限时,
在第四象限时,
①如图(1),请问点![]() 是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
②如图(2),已知点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 这四个点为顶点的四边形是平行四边形时,求点
这四个点为顶点的四边形是平行四边形时,求点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在边长为10的正方形![]() 中,点
中,点![]() 在边
在边![]() 上移动(点
上移动(点![]() 不与点
不与点![]() ,
,![]() 重合),
重合),![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,将正方形
,将正方形![]() 沿
沿![]() 所在直线折叠,则点
所在直线折叠,则点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() ,
,
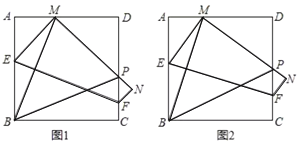
(1)若![]() ,求
,求![]() 的长;
的长;
(2)随着点![]() 在边
在边![]() 上位置的变化,
上位置的变化,![]() 的度数是否发生变化?若变化,请说明理由;若不变,请求出
的度数是否发生变化?若变化,请说明理由;若不变,请求出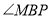 的度数;
的度数;
(3)随着点![]() 在边
在边![]() 上位置的变化,点
上位置的变化,点![]() 在边
在边![]() 上位置也发生变化,若点
上位置也发生变化,若点![]() 恰好为
恰好为![]() 的中点(如图2),求
的中点(如图2),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业投资1000万元引进一条农产品生产线,若不计维修、保养费用,预计投产后每年可创330万元,该生产线投产后,从第一年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx(a≠0),若第一年的维修、保养费为20万元,第二年的为40万元.
(1)求y与x之间的函数表达式;
(2)投产后,这个企业在第几年就能收回投资?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com