


科目:初中数学 来源: 题型:
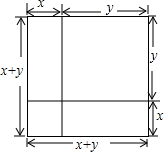 仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是( )
仔细观察图形,依据图形面积间的关系,不添加辅助线,便可得到一个熟悉的公式,这个公式是( )| A、(x-y)2=x2-xy+y2 |
| B、(x-y)2=x2-2xy+y2 |
| C、(x+y)2=x2+2xy+y2 |
| D、(x+y)2=x2+y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
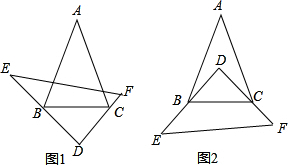
 已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:
 在检测一只汽车轮胎时,先用高压充气泵向其中匀速充气,充满后用于测试,测试结束后打开气门放气,轮胎内气压越大,放气速度快,直至放气结束为至.则下列图象能较好的反应轮胎内气压与时间的关系是( )
在检测一只汽车轮胎时,先用高压充气泵向其中匀速充气,充满后用于测试,测试结束后打开气门放气,轮胎内气压越大,放气速度快,直至放气结束为至.则下列图象能较好的反应轮胎内气压与时间的关系是( )A、 |
B、 |
C、 |
D、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com