
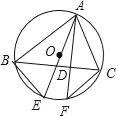
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
【答案】(1)证明见解析;(2)AC=4![]() .
.
【解析】
(1)由BE=CF,则可证得∠BAE=∠FAC,根据圆周角定理和等角的余角相等证明即可;
(2)连接OC,根据圆周角定理证明△AOC是等腰直角三角形,由勾股定理即可求得.
(1)证明:∵BE=CF,
∴弧BE=弧CF,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴ADC=90°,
∴∠FAC+∠ACD=90°,
∵∠E=∠ACB,
∴∠E+∠BAE=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)如图,连接OC,
∴∠AOC=2∠ABC,
∵∠ABC=∠CAE,
∴∠AOC=2∠CAE,
∵OA=OC,
∴∠CAO=∠ACO=![]() ∠AOC,
∠AOC,
∴△AOC是等腰直角三角形,
∵AE=8,
∴AO=CO=4,
∴AC=4![]() .
.


科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,垂足是
,垂足是![]() ,
,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() .
.
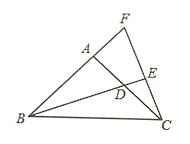
(1)在图中找出与![]() 全等的三角形,并说出全等的理由;
全等的三角形,并说出全等的理由;
(2)说明![]() ;
;
(3)如果![]() ,直接写出
,直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
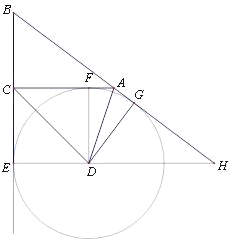
【题目】如图,在△ABC中,BC=a,AC=b,AB=c,⊙D与BC、AC、AB都相切,切点分别是E、F、G,BA、ED的延长线交于点H,a、b是关于x的方程x2﹣(c+4)x+4c+8=0的两个根.
(1)求证:△ABC是直角三角形;
(2)若25asin∠BAC=9c,求四边形CEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
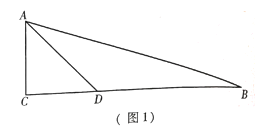
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,连结
上,连结![]() ,且
,且![]() .
.
(1)如图1,求![]() 的度数;
的度数;
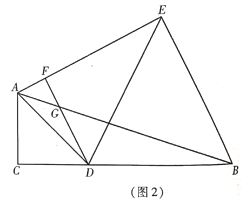
(2) 如图2, 点![]() 在
在![]() 的垂直平分线上,连接
的垂直平分线上,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求证:
,求证: ![]() 是等腰直角三角形;
是等腰直角三角形;
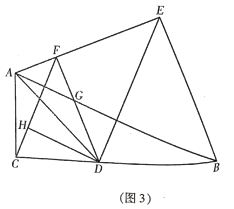
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作 ![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
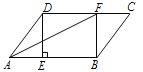
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求□ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com