
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的正半轴上),与
轴的正半轴上),与![]() 轴交于点
轴交于点![]() ,矩形
,矩形![]() 的一条边
的一条边![]() 在线段
在线段![]() 上,顶点
上,顶点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上.
上.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
![]() 当矩形
当矩形![]() 的面积
的面积![]() 取最大值时,
取最大值时,
①求直线![]() 的解析式;
的解析式;
②在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,若点
,若点![]() 恰好落在该抛物线上,则
恰好落在该抛物线上,则![]() ________.
________.
【答案】⑴:![]() ,
,![]() ,
,![]() ;⑵
;⑵![]() ;⑶:①
;⑶:①![]() ;②
;②![]() .
.
【解析】
(1)令x=0求出抛物线与x轴的交点坐标,令x=0求出抛物线与y轴交点坐标;
(2)先表示出BE,DE,用矩形的面积公式求解即可;(3)①由(2)得到的矩形面积的函数关系式,面积最大时求出m,从而确定出D,F坐标,即可得出直线解析式;②先确定出直线DF和抛物线的交点坐标,用比例式求出k.
(1)∵抛物线![]() 与x轴交于A,B两点(点A在x轴的正半轴上),∴令y=0,即
与x轴交于A,B两点(点A在x轴的正半轴上),∴令y=0,即![]() ,∴x=-4或x=2,令
,∴x=-4或x=2,令![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知,OA=2,OC=4,AD=2-m,∵DG∥OC,∴![]() ,∴DG=4-2m,同理BE=4-2m,∴DE=AB-AD-BE=3m,∴
,∴DG=4-2m,同理BE=4-2m,∴DE=AB-AD-BE=3m,∴![]() ;
;
(3)①由(2)得,![]() ;当m=1时,矩形DEFG面积最大,最大面积为6,此时,
;当m=1时,矩形DEFG面积最大,最大面积为6,此时,![]() ,
,![]() ,
,![]() ,
,![]() ,∴直线DF的解析式为
,∴直线DF的解析式为![]() ;
;
②如图
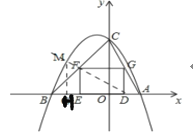
由①知,D(1,0),F(-2,2),∴![]() ,∴FM=k×DF=
,∴FM=k×DF=![]() ,过点M作MH⊥x轴,设
,过点M作MH⊥x轴,设![]() 则
则![]() ∴
∴![]() ,∵点M在抛物线上,∴
,∵点M在抛物线上,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故答案为
,故答案为![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,5),点B为y轴正半轴上一动点,以BP为边作如图所示等边△PBC.CA的延长线交x轴交于E.
(1)求证:OB=AC;
(2)求∠CAP的度数;
(3)当B点运动时,AE的长度是否发生变化?若不发生变化,请求出AE的值,若发生变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
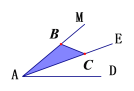
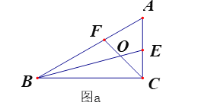
(2)如图a,在△ABC中, ∠ACB=![]() ,∠A=
,∠A=![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
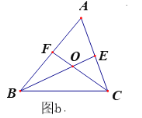
(3)如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至点G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是 ( )

A.8+2aB.8aC.6+aD.6+2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣12n+36+|n﹣2m|=0.

(1)求A、B两点的坐标;
(2)若点D为AB中点,延长DE交x轴于点F,在ED的延长线上取点G,使DG=DF,连接BG.
①BG与y轴的位置关系怎样?说明理由; ②求OF的长;
(3)如图2,若点F的坐标为(10,10),E是y轴的正半轴上一动点,P是直线AB上一点,且P的横坐标为6,是否存在点E使△EFP为等腰直角三角形?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com