
【题目】如图,已知二次函数 ![]() 的图像过点A(-4,3),B(4,4).
的图像过点A(-4,3),B(4,4).

(1)求抛物线二次函数的解析式.
(2)求一次函数直线AB的解析式.
(3)看图直接写出一次函数直线AB的函数值大于二次函数的函数值的x的取值范围.
(4)求证:△ACB是直角三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)﹣4﹤x﹤4;(4)见解析
;(3)﹣4﹤x﹤4;(4)见解析
【解析】
(1)由题意把A点或B点坐标代入得到![]() ,即可得出抛物线二次函数的解析式;
,即可得出抛物线二次函数的解析式;
(2)根据题意把A点或B点坐标代入y=kx+b,利用待定系数法即可求出一次函数直线AB的解析式;
(3)由题意观察函数图像,根据y轴方向直线在曲线上方时,进而得出x的取值范围;
(4)根据题意求出C点坐标,进而由两点的距离公式或者是构造直角三角形进行分析求证即可.
解:(1)把A点或B点坐标代入得到![]() ,
,
∴抛物线二次函数的解析式为:![]() .
.
(2)把A点或B点坐标代入y=kx+b列出方程组![]() ,解得
,解得![]() ,
,
得出一次函数直线AB的解析式为:.![]() .
.
(3)由图象可以看出:一次函数直线AB的函数值大于二次函数的函数值的x的取值范围为:﹣4﹤x﹤4.
(4)由抛物线的表达式得:C点坐标为(-2,0),
由两点的距离公式或者是构造直角三角形得出,
![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴△ACB是直角三角形.


科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
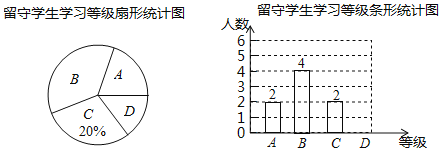
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在
上的所有点都在![]() 的内部或边长,则称
的内部或边长,则称![]() 为
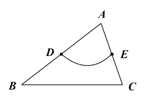
为![]() 的中内弧.例如下图中
的中内弧.例如下图中![]() 是
是![]() 的一条中内弧.
的一条中内弧.
(1)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.画出
的中点.画出![]() 的最长的中内弧
的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
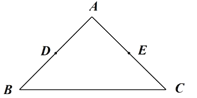
(2)在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
①若![]() ,直接写出
,直接写出![]() 的中内弧
的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;
②若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,直接写出
的内部或边长,直接写出![]() 的取值范围;
的取值范围;
③若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,则
的内部或边长,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一种水果的成本价是5元/千克,在销售中发现,当这种水果的价格定为7元/千克时,每天可以卖出160千克,在此基础上,这种水果的单价每提高1元/千克,该水果店每天就会少卖出20千克,设这种水果的单价为![]() 元(
元(![]() ),
),
(1)请用含![]() 的代数式表示:每千克水果的利润 元及每天的销售量 千克.
的代数式表示:每千克水果的利润 元及每天的销售量 千克.
(2)若该水果店一天销售这种水果所获得的利润是420元,为了让利于顾客,单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格.某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A,B,C,D表示,并将测试结果绘制成如图两幅不完整的统计图.

请根据统计图中的信息解答以下问题:
(1)本次抽取的学生人数是 ,扇形统计图中A所对应扇形圆心角的度数是 .
(2)把条形统计图补充完整.
(3)若该学校共有2800人,等级达到优秀的人数大约有多少?
(4)A等级的4名学生中有3名女生1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
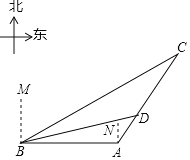
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC .
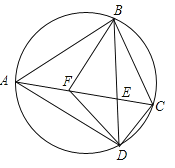
(1)若∠DFC=40,求∠CBF的度数.
(2)求证: CD⊥DF .
查看答案和解析>>
科目:初中数学 来源: 题型:
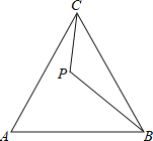
【题目】如图所示,点P位于等边△ABC的内部,且∠ACP=∠CBP.
(1)延长BP至点D,使得PD=PC,连接AD,CD.
①依题意,补全图形;
②证明:AD+CD=BD;
(2)在(1)的条件下,若BD的长为2,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com