
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

【答案】64° 32°
【解析】
(1)由∠BAC=100°,可求出∠ABC=∠ACB=40°,当∠DAC=36°时,根据∠BAD=∠BAC-∠DAC可求出∠BAD的度数,根据等腰三角形的性质求出∠ADE=∠AED的度数,再根据三角形的外角的性质求解.
(2) 由思路(1)可知∠ABC=∠ACB=40°,以及∠ADE=∠AED=![]() ,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
(3)根据(1)的思路,可知∠ABC=∠ACB=40°,∠ADE=∠AED=![]() ,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
(1)∠BAD=∠BAC-∠DAC=100°-36°=64°.
∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,
∴∠ABC=∠ACB=40°,
∴∠ADC=∠ABC+∠BAD=40°+64°=104°.
∵∠DAC=36°,∠ADE=∠AED,
∴∠ADE=∠AED=72°,
∴∠CDE=∠ADC-∠ADE=104°-72°=32°.
故答案为64°,32°.
(2)∠BAD=2∠CDE,理由如下:
如图(2),在△ABC中,∠BAC=100°,
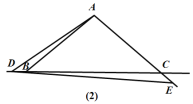
∴∠ABC=∠ACB=40°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACB=∠CDE+∠AED,
∴∠CDE=∠ACB-∠AED=40°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=n-100°,
∴∠BAD=2∠CDE;
(3)∠BAD=2∠CDE,理由如下:
如图(3),在△ABC中,∠BAC=100°,
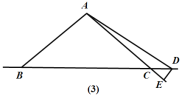
∴∠ABC=∠ACB=40°,
∴∠ACD=140°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACD=∠CDE+∠AED,
∴∠CDE=∠ACD-∠AED=140°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=100°+n,
∴∠BAD=2∠CDE.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
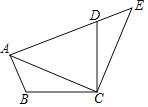
A. 55°B. 60°C. 65°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣![]() 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,求证:
,求证:![]() ,请将证明过程填写完整.
,请将证明过程填写完整.
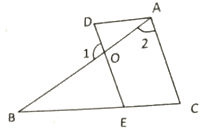
证明:∵![]() (已知)
(已知)
又∵![]() ( )
( )
∴________![]() ,
,
∴![]() ____________( )
____________( )
∴![]() ______________( )
______________( )
又∵![]() (已知)
(已知)
∴![]() ________________,
________________,
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )

A. 65°B. 60°C. 50°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种产品,每件产品的成本为2400元,销售单价定位3000元,该商场为了促销,规定客户一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元;
(1)设一次购买这种产品x(x≥10)件,商场所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(2)在客户购买产品的件数尽可能少的前提下,商场所获的利润为12000元,此时该商场销售了多少件产品?
(3)填空:该商场的销售人员发现,当客户一次购买产品的件数在某一个区间时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,客户一次购买产品的数量x满足的条件是 (其它销售条件不变)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com