
分析 根据分式的混合运算顺序和运算法则将除法转化成乘法,进行约分计算,由非负数之和为0,两非负数分别为0求出a与b的值,代入计算即可得到结果.
解答 解:∵$\sqrt{\frac{{a}^{2}-1}{{a}^{2}+a}}+2{a}^{2}+8{b}^{4}-8a{b}^{2}=0$,
∴$\sqrt{\frac{a-1}{a}}+2(a-2{b}^{2})^{2}$=0,
∵$\sqrt{\frac{a-1}{a}}$、2(a-2b2)2是非负数,
∴a-1=0,a-2b2=0,
∴a=1,b=±$\frac{\sqrt{2}}{2}$,
∴原式=$\frac{4{a}^{2}}{{b}^{2}}$•$\frac{b}{a-2}$-$\frac{4a}{b}$
=$\frac{4{a}^{2}}{b(a-2)}$-$\frac{4a}{b}$
=$\frac{4{a}^{2}}{b(a-2)}$-$\frac{4a}{b(a-2)}$
=$\frac{4a(a-1)}{b(a-2)}$
=O.
点评 此题考查了分式的化简求值,以及非负数的性质,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.


科目:初中数学 来源: 题型:解答题
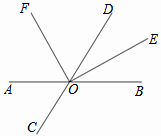 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
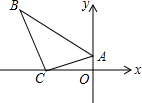 一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为( )
一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为( )| A. | (-3-$\sqrt{3}$,3) | B. | (-3-$\sqrt{3}$,3$\sqrt{3}$) | C. | (-$\sqrt{3}$,3) | D. | (-$\sqrt{3}$,3$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
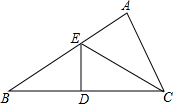 如图,已知△ABC,AB=10,BC边的垂直平分线交AB、BC于点E、D,AC=6,则△ACE的周长是( )
如图,已知△ABC,AB=10,BC边的垂直平分线交AB、BC于点E、D,AC=6,则△ACE的周长是( )| A. | 13 | B. | 16 | C. | 11 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com