Question

19．如图1，△ABC中，∠BAC=60°，O是△ABC内一点，△ABO≌△ACD，连接OD．
（1）求证：△AOD为等边三角形；
（2）如图2，连接OC，若∠BOC=130°，∠AOB=∠α．
①求∠OCD的度数；
②当△OCD是等腰三角形时，求∠α的度数．

Answer 1

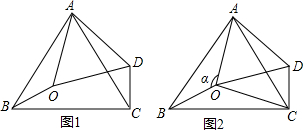
分析 （1）根据全等三角形得到AO=AD，∠BAO=∠CAD，由∠BAC=60°，求得∠OAD=60°，即可得到结论；
（2）①根据△AOD为等边三角形，求得∠AOD=∠ADO=60°，求得∠DOC=360°-α-130°-60°=170°-α，根据全等三角形的性质得到∠ADC=∠AOB=α，于是得到∠OCD=180°-∠DOC-∠ODC=70°；②当△OCD是等腰三角形时，（Ⅰ）当OD=OC，由∠DOC=170°-α，得到∠OCD=∠ODC=$\frac{180°-∠COD}{2}$=$\frac{1}{2}α+5°$，列方程得到α=130°（Ⅱ）当OD=CD，于是得到∠OCD=∠COD=170°-α；求得∠ODC=180°-2×170°+2α=2α-160°，列方程即可得到α=100°；（Ⅲ）当OC=CD，于是得到∠ODC=∠COD=170°-α，列方程即可得到α=115°．

解答 解：（1）∵△ABO≌△ACD，
∴AO=AD，∠BAO=∠CAD，
∵∠BAC=60°，
∴∠OAD=60°，
∴△AOD为等边三角形；

（2）①∵△AOD为等边三角形，
∴∠AOD=∠ADO=60°，
∵∠BOC=130°，∠AOB=∠α，
∴∠DOC=360°-α-130°-60°=170°-α，
∵△ABO≌△ACD，
∴∠ADC=∠AOB=α，
∴∠ODC=α-60°，
∴∠OCD=180°-∠DOC-∠ODC=70°；
②当△OCD是等腰三角形时，
（Ⅰ）当OD=OC，∵∠DOC=170°-α，
∴∠OCD=∠ODC=$\frac{180°-∠COD}{2}$=$\frac{1}{2}α+5°$，
∴60°+$\frac{1}{2}α+5°$=α，
解得：α=130°
（Ⅱ）当OD=CD，∴∠OCD=∠COD=170°-α；
∴∠ODC=180°-2×170°+2α=2α-160°，
∴60°+2α-160°=α，
解得：α=100°；
（Ⅲ）当OC=CD，∴∠ODC=∠COD=170°-α，
∴170°-α+60°=α，
解得：α=115°．
综上所述：当△OCD是等腰三角形时，∠α的度数为：130°，100°，115°．

点评 本题考查了全等三角形的性质，等边三角形的判定，等腰三角形的判定和性质，熟练掌握全等三角形的性质定理是解题的关键．