
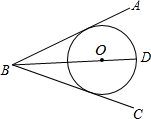
 已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切.
已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
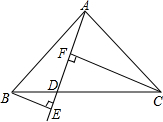 如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.
如图,画出一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B,C作射线AD的垂线BE和CF,垂足分别为E,F,量出BE,CF,EF的长,改变D的位置,再重复上面的操作,你是否发现BE,CF,EF的长度之间有某种关系?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
| 与标准质量的差值(单位:克) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com