
【题目】如图,对称轴为直线x=![]() 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)①E(2,﹣2),②△ABE是直角三角形;(3)存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).
x﹣3;(2)①E(2,﹣2),②△ABE是直角三角形;(3)存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).
【解析】试题分析:
(1)由抛物线的对称轴为直线![]() ,与
,与![]() 轴交于A、B两点(点A在点B的左侧),AB=5,可得点A、B的坐标分别为(﹣2,0),B(3,0),由此可设抛物线解析式为:
轴交于A、B两点(点A在点B的左侧),AB=5,可得点A、B的坐标分别为(﹣2,0),B(3,0),由此可设抛物线解析式为: ![]() ,再代入点C(0,-3)解出
,再代入点C(0,-3)解出![]() 的值即可求得解析式;
的值即可求得解析式;
(2)①根据线段中点坐标公式由点B、C的坐标可得点D的坐标,由点D的坐标可求得直线OD的解析式;解有OD的解析式和抛物线的解析式组成的方程组即可得到点E的坐标;
②由点A、B、E的坐标可求出AB、BE、AE的长度,根据勾股定理逆定理可判断出△ABE是直角三角形;
(3)过点E作EP∥OB交抛物线于点P,根据点P和E关于直线![]() 对称,求得点P的坐标,进一步可求得PE的长,若PE=OB,则点P符合要求,否则就不存在符合要求的点P.
对称,求得点P的坐标,进一步可求得PE的长,若PE=OB,则点P符合要求,否则就不存在符合要求的点P.
试题解析:
(1)∵点A、B关于对称轴![]() 对称,且AB=5
对称,且AB=5
∴A(﹣2,0),B(3,0),
∴可设抛物线的解析式为: ![]() ,
,
把点C的坐标(0,﹣3)代入得: ![]() ,解得:
,解得: ![]() ,
,
∴该二次函数的解析式为: ![]() ,即
,即![]() ;
;
(2)①∵点B、C的坐标分别为:(3,0),(0,﹣3),
∴线段BC的中点D的坐标为: ![]() .
.
设直线OE的解析式为: ![]() ,
,
把 D![]() ,代入
,代入![]() 解得:
解得: ![]() ,
,
∴OE的解析式为: ![]() ,
,
由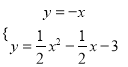 ,解得
,解得![]() ,
, ![]() ,
,
又因为点E在第四象限,
∴E的坐标为(2,﹣2).
②∵AE=![]() ,BE=
,BE=![]() ,AB=5,
,AB=5,
∴AB2=AE2+BE2,
∴△ABE是直角三角形;
(3)存在满足条件的点P
过E作PE∥OB,交抛物线于点P,
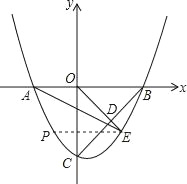
∵点P和点E(2,﹣2)关于对称轴![]() 对称
对称
∴P的坐标为(﹣1,﹣2),
∴PE=3=OB,
又∵PE∥OB,
∴四边形OBEP是平行四边形,
∴存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )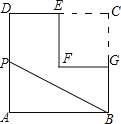
A. 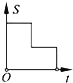
B. 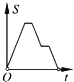
C. 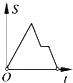
D. 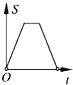
查看答案和解析>>
科目:初中数学 来源: 题型:
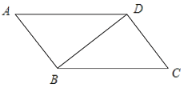
【题目】如图,已知![]() 为
为![]() 的一条对角线.
的一条对角线.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①作![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 于点
于点![]() ;
;
②连接![]() ,
,![]() ;
;
(2)猜想与证明:试猜想四边形![]() 是哪种特殊的四边形,并说明理由.
是哪种特殊的四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1 240元,3辆甲种客车和2辆乙种客车共需租金1 760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com