
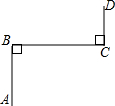
 如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.
如图,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是AB∥CD.  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
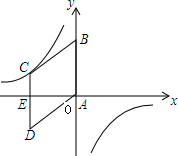 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),边CD与x轴交于点E.
如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),边CD与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $-\frac{5}{13}$ | D. | $-\frac{13}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=3米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com