
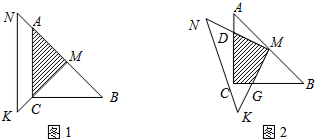
分析 (1)连接CM,根据等腰直角三角形的性质得出AM=CM=BM,∠MCB=∠A=45°,∠CMA=90°,求出∠AMD=∠CMG,根据ASA推出△ADM≌△CGM,求出S△ADM=S△CGM,即可推出重叠部分MDCG的面积=S△ACM=$\frac{1}{2}$S△ABC,求出△ABC的面积即可;
(2)连接CM,根据等腰直角三角形的性质得出AM=CM=BM,∠MCB=∠A=45°,∠CMA=90°,求出∠AMD=∠CMG,根据ASA推出△ADM≌△CGM,求出S△ADM=S△CGM,即可推出重叠部分MDCG的面积=S△ACM=$\frac{1}{2}$S△ABC,求出△ABC的面积即可;
(3)设AD=CG=x,则CD=4-x,在Rt△DCG中,由勾股定理得出DG=$\sqrt{C{D}^{2}+C{G}^{2}}$=$\sqrt{(4-x)^{2}+{x}^{2}}$=$\sqrt{2(x-2)^{2}+8}$,即可得出答案.
解答 解:(1)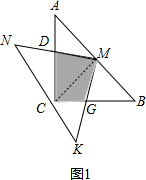
连接CM,
∵△ACB是等腰直角三角形,M为斜边AB的中点,
∴AM=CM=BM,∠MCB=∠A=45°,∠CMA=90°,
∵∠GMD=90°,
∴∠AMD=∠CMG=90°-∠DMC,
在△ADM和△CGM中
$\left\{\begin{array}{l}{∠A=∠MCG}\\{AM=CM}\\{∠AMD=∠CMG}\end{array}\right.$
∴△ADM≌△CGM(ASA),
∴S△ADM=S△CGM,
∴重叠部分MDCG的面积
S=S△DCM+S△CGM
=S△DCM+S△ADM
=S△ACM=$\frac{1}{2}$S△ABC
=$\frac{1}{2}$×4×4
=8;
(2)△MNK在绕定点旋转的过程中,保持与MN与AC有交点D,MK与BC有交点G,四边形MDCG的面积不会改变,
理由是:连接CM,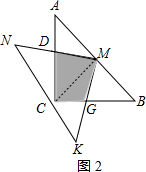
∵△ACB是等腰直角三角形,M为斜边AB的中点,
∴AM=CM=BM,∠MCB=∠A=45°,∠CMA=90°,
∵∠GMD=90°,
∴∠AMD=∠CMG=90°-∠DMC,
在△ADM和△CGM中
$\left\{\begin{array}{l}{∠A=∠MCG}\\{AM=CM}\\{∠AMD=∠CMG}\end{array}\right.$
∴△ADM≌△CGM(ASA),
∴S△ADM=S△CGM,
∴重叠部分MDCG的面积:
S=S△DCM+S△CGM
=S△DCM+S△ADM
=S△ACM
=$\frac{1}{2}$S△ABC
=$\frac{1}{2}$×4×4
=8;
(3)设AD=CG=x,则CD=4-x,
在Rt△DCG中,由勾股定理得:DG=$\sqrt{C{D}^{2}+C{G}^{2}}$=$\sqrt{(4-x)^{2}+{x}^{2}}$=$\sqrt{2(x-2)^{2}+8}$,
当x-2=0,即x=2时,DG最小,最小值是$\sqrt{8}$=2$\sqrt{2}$;
此时重叠部分MDCG的周长是2+2+2+2=8.
点评 此题考查了等腰直角三角形,全等三角形的性质和判定,二次函数的最值,勾股定理的应用,利用等腰直角三角形的性质,等腰直角三角形的面积公式,全等三角形的判定和性质求解.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
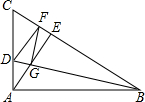 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com