
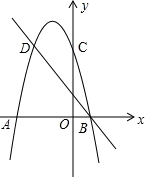
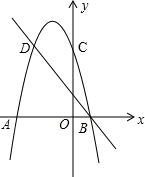
如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【考点】抛物线与x轴的交点;待定系数法求二次函数解析式;二次函数与不等式(组).
【专题】待定系数法.
【分析】(1)根据抛物线的对称性来求点D的坐标;
(2)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),把点A、B、C的坐标分别代入函数解析式,列出关于系数a、b、c的方程组,通过解方程组求得它们的值即可;
(3)根据图象直接写出答案.
【解答】解:(1)∵如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,
∴对称轴是x=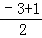 =﹣1.
=﹣1.
又点C(0,3),点C、D是二次函数图象上的一对对称点,
∴D(﹣2,3);
(2)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),
根据题意得 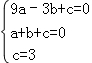 ,
,
解得 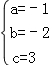 ,
,
所以二次函数的解析式为y=﹣x2﹣2x+3;
(3)如图,一次函数值大于二次函数值的x的取值范围是x<﹣2或x>1.
【点评】本题考查了抛物线与x轴的交点,待定系数法求二次函数解析式以及二次函数与不等式组.解题时,要注意数形结合数学思想的应用.另外,利用待定系数法求二次函数解析式时,也可以采用顶点式方程.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,则S△DEF:S△BCF等于( )
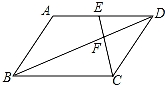
A.1:2 B.1:4 C.1:9 D.4:9
查看答案和解析>>
科目:初中数学 来源: 题型:
某电器厂五月份生产液晶电视5000台,因市场销售业绩不佳,产品严重积压,以致六月份的产量减少了10%,后调整定价,并在电视台做广告,结果销量持续攀升,于是该厂从七月份起产量开始上升,八月份达到6480台,那么该厂七、八月份的产量平均增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
小明在参加区运动会前刻苦进行100米跑训练,老师对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则老师需要知道他这10次成绩的( )
A.众数 B.方差 C.平均数 D.频数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com