
分析 在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,第一次是从甲地驶往乙地时,快车追上慢车,根据追上时快车行驶的路程=慢车行驶的路程列方程求解;第二次是快车到达乙地后返回甲地时与慢车相遇,根据相遇时快车行驶的路程+慢车行驶的路程=甲、乙两地之间的路程×2列方程求解.
解答 解:设从甲地驶往乙地时,快车行驶x小时追上慢车,由题意得
120x=80(x+1),
解得x=2,
则慢车行驶了3小时.
设在整个程中,慢车行驶了y小时,则快车行驶了(y-1-$\frac{20}{60}$)小时,由题意得
120(y-1-$\frac{20}{60}$)+80y=720×2,
解得y=8,
8-3=5(小时).
答:在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是5小时.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
 探究实验:《钟面上的数字》
探究实验:《钟面上的数字》查看答案和解析>>
科目:初中数学 来源: 题型:解答题
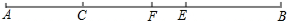 如图,已知线段AB=32,C为线段AB上一点,且AC=$\frac{1}{3}$BC,E为线段BC的中点,F为线段AB的中点,求线段EF的长.
如图,已知线段AB=32,C为线段AB上一点,且AC=$\frac{1}{3}$BC,E为线段BC的中点,F为线段AB的中点,求线段EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
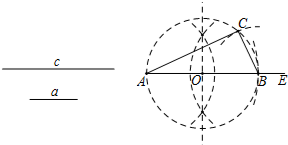
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
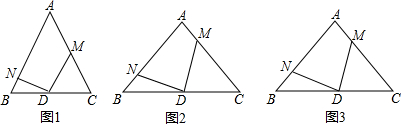
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com