
ЁОЬтФПЁПвбжЊШчЭМЃЌдкОиаЮABCDжаЃЌAB=6cmЃЌBC=8cmЃЌЖдНЧЯпACЃЌBDНЛгкЕу0ЃЎЕуPДгЕуAГіЗЂЃЌбиADЗНЯђЯђжеЕуDдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() cm/sЃЛЭЌЪБЃЌЕуQДгЕуDГіЗЂЃЌбиDCЗНЯђЯђжеЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЛЕБвЛИіЕуЭЃжЙдЫЖЏЪБЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЎСЌНгPOВЂбгГЄЃЌНЛBCгкЕуEЃЌЙ§ЕуQзїQF//ACЃЌНЛBDгкЕуFЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌНтД№ЯТСаЮЪЬтЃК
cm/sЃЛЭЌЪБЃЌЕуQДгЕуDГіЗЂЃЌбиDCЗНЯђЯђжеЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ1cm/sЃЛЕБвЛИіЕуЭЃжЙдЫЖЏЪБЃЌСэвЛИіЕувВЭЃжЙдЫЖЏЃЎСЌНгPOВЂбгГЄЃЌНЛBCгкЕуEЃЌЙ§ЕуQзїQF//ACЃЌНЛBDгкЕуFЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌНтД№ЯТСаЮЪЬтЃК
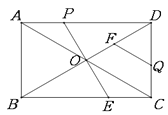
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAOPЪЧЕШбќШ§НЧаЮЃП
ЃЈ2ЃЉЩшЮхБпаЮOECQFЕФУцЛ§ЮЊSЃЈcm2ЃЉЃЌЪдШЗЖЈSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙSЮхБпаЮSЮхБпаЮOECQFЃКSЁїACD=9ЃК16ЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЁОД№АИЁП(1) t=![]() Лђt=5 (2) S=
Лђt=5 (2) S=![]() (3) t=3Лђt=
(3) t=3Лђt=![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЃЌИљОнОиаЮЕФаджЪКЭЙДЙЩЖЈРэЕУЕНAC=10cmЃЌЂйЕБAP=PO=tЃЌЙ§PзїPMЁЭAOЃЌДгЖјЕУЕНAMЃЌжЄУїЁїAPMЁзЁїACDЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУЕНAP=tЕФжЕЃЌдйИљОнЬтвтжБНгЕУЕНЕкЖўжжТњзуЬтвтЕФtжЕЃЛ
ЃЈ2ЃЉЃЌЙ§ЕуOзїOHЁЭBCНЛBCгкЕуHЃЌИљОнОиаЮЕФаджЪжЄУїЁїDOPЁеЁїBOEЃЌЕУЕНBE=PD=8-tЃЌДгЖјЕУЕНЁїBOEЕФУцЛ§ЃЛ
ИљОнFQЁЮACЃЌжЄЕУЁїDFQЁзЁїDOCЃЌгЩЯрЫЦШ§НЧаЮЕФУцЛ§БШПЩЧѓЕУЁїDFQЕФУцЛ§ЃЌДгЖјПЩЧѓЮхБпаЮOECQFЕФУцЛ§ЃЛ
ЃЈ3ЃЉЃЌгЩЃЈ2ЃЉПЩЕУЮхБпаЮOECQFЕФУцЛ§ЃЌИљОнSЮхБпаЮOECQFЃКSЁїACD=9:16СаЗНГЬЃЌЖдЗНГЬНјааЧѓНтМДПЩЕУГіНсТл.
ЃЈ1ЃЉЁпдкОиаЮABCDжаЃЌAB=6cmЃЌBC=8cmЃЌ
ЁрAC=10cmЃЌ
ЂйЕБAP=PO=tЃЌШчЭМ1ЃЌ

Й§PзїPMЁЭAOЃЌ
ЁрAM=![]() AO=
AO=![]() .
.
ЁпЁЯPMA=ЁЯADC=90ЁуЃЌЁЯPAM=ЁЯCADЃЌ
ЁрЁїAPMЁзЁїACDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAP=t=![]() ЃЛ
ЃЛ
ЂкЕБAP=AO=t=5ЪБЃЌЁїAOPЮЊЕШбќШ§НЧаЮ.
злЩЯЫљЪіЃЌЕБtЮЊ![]() Лђ5ЪБЃЌЁїAOPЪЧЕШбќШ§НЧаЮ.
Лђ5ЪБЃЌЁїAOPЪЧЕШбќШ§НЧаЮ.
ЃЈ2ЃЉЙ§ЕуOзїOHЁЭBCНЛBCгкЕуHЃЌдђOH=![]() CD=
CD=![]() AB=3cmЃЎ
AB=3cmЃЎ
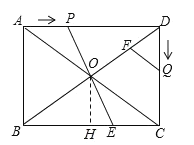
гЩОиаЮЕФаджЪПЩжЊЁЯPDO=ЁЯEBOЃЌDO=BOЃЌгжЕУЁЯDOP=ЁЯBOEЃЌ
ЁрЁїDOPЁеЁїBOEЃЌ
ЁрBE=PD=8-tЃЌ
дђSЁїBOE=![]() BEЁЄOH=
BEЁЄOH=![]() ЁС3ЁС(8-t)=12-
ЁС3ЁС(8-t)=12-![]() t.
t.
ЁпFQЁЮACЃЌ
ЁрЁїDFQЁзЁїDOCЃЌЯрЫЦБШЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпSЁїDOC=![]() SОиаЮABCD=
SОиаЮABCD=![]() ЁС6ЁС8=12
ЁС6ЁС8=12![]() ЃЌ
ЃЌ
ЁрSЁїDFQ=![]() =
=![]() ЃЌ
ЃЌ
ЁрSЮхБпаЮOECQF=SЁїDBC-SЁїBOE-SЁїDFQ=
![]() ЃЛ
ЃЛ
ЁрSгыtЕФКЏЪ§ЙиЯЕЪНЮЊS=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдк.
ЁпSЁїACD=![]() ЁС6ЁС8=24ЃЌ
ЁС6ЁС8=24ЃЌ
ЁрSЮхБпаЮOECQFЃКSЁїACD=(![]() ):24=9:16ЃЌ
):24=9:16ЃЌ
НтЕУt=3Лђt=![]() ЃЌ
ЃЌ
Ёрt=3Лђ![]() ЪБЃЌSЮхБпаЮOECQF:SЁїACD=9:16.
ЪБЃЌSЮхБпаЮOECQF:SЁїACD=9:16.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
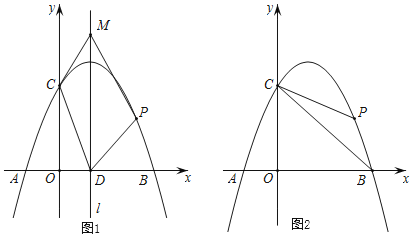
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпy=Љx2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкCЕуЃЌЕуPЪЧХзЮяЯпЩЯдкЕквЛЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕуPЕФКсзјБъЮЊtЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсЮЊlЃЌlгыxжсЕФНЛЕуЮЊDЃЎдкжБЯпlЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгBCЃЌPBЃЌPCЃЌЩшЁїPBCЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкtЕФКЏЪ§БэДяЪНЃЛ
ЂкЧѓPЕуЕНжБЯпBCЕФОрРыЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
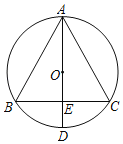
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌADЮЊЁбOЕФжБОЖЃЌADгыBCЯрНЛгкЕуEЃЌЧвBEЃНCEЃЎ
ЃЈ1ЃЉЧыХаЖЯADгыBCЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєBCЃН6ЃЌEDЃН2ЃЌЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃН![]() гыxжсНЛгкAЁЂBСНЕуЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЁЯCODЃН60ЁуЃЌЧвODЃНOCЃЎ
гыxжсНЛгкAЁЂBСНЕуЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЁЯCODЃН60ЁуЃЌЧвODЃНOCЃЎ
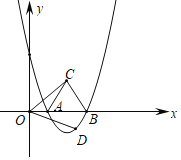
ЃЈ1ЃЉAЕузјБъЮЊЁЁ ЁЁЃЌBЕузјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧѓжЄЃКЕуDдкХзЮяЯпЩЯЃЛ
ЃЈ3ЃЉЕуMдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЕуNдкХзЮяЯпЩЯЃЌШєвдMЁЂNЁЂOЁЂDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШЅФъЕФДДНЈШЋЙњЮФУїГЧЪаЛюЖЏжаЃЌБЇзХЮвЮЊЮФУїШ№АВГівЛЗнСІЕФЯыЗЈЃЌаЁЛЊОЭЙЋжкЖддкВЭЬќЮќбЬЕФЬЌЖШНјааСЫЫцЛњГщбљЕїВщЃЌжївЊгаЫФжжЬЌЖШЃКAЁЂЙЫПЭГіУцжЦжЙЃЛBЁЂШАЫЕНјЮќбЬЪвЃЛCЁЂВЭЬќРЯАхГіУцжЦжЙЃЛDЁЂЮоЫљЮНЃЎЫћНЋЕїВщНсЙћЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭМжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉетДЮГщбљЕФЙЋжкга__________ШЫЃЛ
ЃЈ2ЃЉЧыНЋЭГМЦЭМЂйВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЭГМЦЭМЂкжаЃЌЁАЮоЫљЮНЁБВПЗжЫљЖдгІЕФдВаФНЧЪЧЖрЩйЖШЃП
ЃЈ4ЃЉШєШ№АВШЋЪаШЫПкга120ЭђШЫЃЌЙРМЦдоГЩЁАВЭЬќРЯАхГіУцжЦжЙЁБЕФгаЖрЩйЭђШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЌAEЪЧЁбOЕФжБОЖЃЌAFЪЧЁбOЕФЯвЃЌAFЁЭBCЃЌДЙзуЮЊD.
ЃЈ1ЃЉЧѓжЄЃКЁЯBAE=ЁЯCAD.
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ4ЃЌAC=5ЃЌCD=2ЃЌЧѓCF.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ ЁїABC ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ A(-2,3)ЁЂB(-6,0)ЁЂC(-1,0).
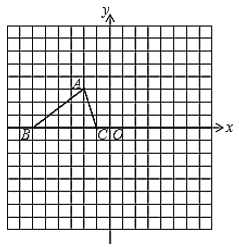
ЃЈ1ЃЉНЋЁїABCШЦзјБъдЕуOФцЪБеыа§зЊ 90Ёу. ЛГіЭМаЮЃЌжБНгаДГіЕуBЕФЖдгІЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧыжБНгаДГіЃКвд AЁЂBЁЂC ЮЊЖЅЕуЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕу D ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄвЛЖЈЕФе§ЗНаЮABCDЃЌQЮЊCDЩЯвЛИіЖЏЕуЃЌAQНЛBDгкЕуMЃЌЙ§MзїMNЁЭAQНЛBCгкЕуNЃЌзїNPЁЭBDгкЕуPЃЌСЌНгNQЃЌЯТСаНсТлЃКЂйAM=MNЃЛЂкMP=![]() BDЃЛЂлBN+DQ=NQЃЛЂм
BDЃЛЂлBN+DQ=NQЃЛЂм![]() ЮЊЖЈжЕЃЎЦфжавЛЖЈГЩСЂЕФЪЧ
ЮЊЖЈжЕЃЎЦфжавЛЖЈГЩСЂЕФЪЧ

A. ЂйЂкЂл B. ЂйЂкЂм C. ЂкЂлЂм D. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊСНИіЙВвЛИіЖЅЕуЕФЕШбќRtЁїABCЃЌRtЁїCEFЃЌЁЯABC=ЁЯCEF=90ЁуЃЌСЌНгAFЃЌMЪЧAFЕФжаЕуЃЌСЌНгMBЁЂMEЃЎ
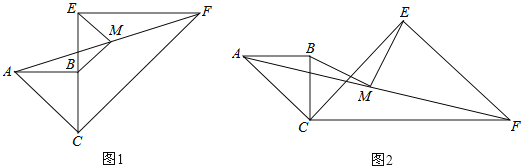
ЃЈ1ЃЉШчЭМ1ЃЌЕБCBгыCEдкЭЌвЛжБЯпЩЯЪБЃЌЧѓжЄЃКMBЁЮCFЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєCB=aЃЌCE=2aЃЌЧѓBMЃЌMEЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЁЯBCE=45ЁуЪБЃЌЧѓжЄЃКBM=MEЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com