
分析 (1)直接根据概率公式求解;
(2)由于每个年级都要有作品获一等奖,则九年级有两件获一等奖,七年级有一件获一等奖,八年级有一件获一等奖,于是可画树状图展示所有12种等可能的结果数,再找出抽出两件作品中一件是七年级、另一件是九年级学生作品的结果数,然后根据概率公式求解.
解答 解:(1)随机抽出一件作品是九年级学生作品的概率=$\frac{20}{50}$=$\frac{2}{5}$;
(2)九年级有两件获一等奖,七年级有一件获一等奖,八年级有一件获一等奖,
画树状图: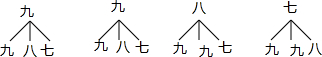
共有12种等可能的结果数,其中抽出两件作品中一件是七年级、另一件是九年级学生作品的结果数为4,
所以抽出两件作品中一件是七年级、另一件是九年级学生作品的概率=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
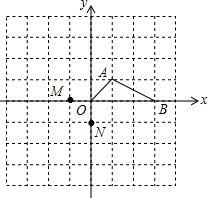 如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.
如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
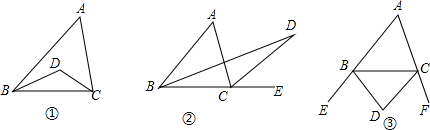
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com