
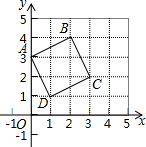
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )| A. | (-1,-4) | B. | (2,4) | C. | (-1,-4) | D. | (1,4) |
分析 根据已知,将点B关于x轴、y轴对称,然后将所得点向右平移一个单位,在进行第二次变化,变化完毕发现经过两次变化,点B回到原来位置,因此可以断定点B经过偶次变化都会回到原来位置,因此经过10次变化,B点仍会回到原来位置.
解答 解:根据题意
第一次变化:B(2,4)关于x轴对称得(2,-4),关于y轴对称得(-2,-4),向右平移一个单位得(-1,-4),
第二次变化:B(-1,-4)关于x轴对称得(-1,4),关于y轴对称得(1,4),向右平移一个单位得(2,4),
可以发现经过两次变化,点B回到原来位置.
故10次变化后B点将回到(2,4).
故选:B
点评 本题考查了点的坐标的变化,通过变化要求学生掌握点关于对称轴变化的规律及平移规律.此外学生应该根据点的对称找到一些点的坐标的变化规律.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
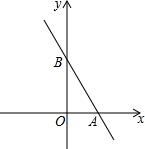 如图,直线l的解析式为y=$-\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
如图,直线l的解析式为y=$-\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
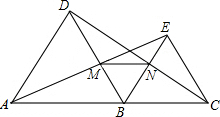 如图,B为线段AC上一动点(点B不与点A、C重合),在AC的同侧分别作等边△ABD和等边△BCE,AE与BD相交于点M,BE与CD相交于点N,连接MN.求证:(1)BM=BN;(2)MN∥AC.
如图,B为线段AC上一动点(点B不与点A、C重合),在AC的同侧分别作等边△ABD和等边△BCE,AE与BD相交于点M,BE与CD相交于点N,连接MN.求证:(1)BM=BN;(2)MN∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
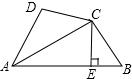 如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=$\frac{1}{2}$(AB+AD).
如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=$\frac{1}{2}$(AB+AD).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com