
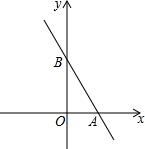 如图,直线l的解析式为y=$-\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
如图,直线l的解析式为y=$-\frac{4}{3}$x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).分析 (1)利用点B代入直线,求出直线解析式,然后求直线与x轴交点坐标;
(2)已知点到直线距离,可以做点到直线的垂线,构造直角三角形,利用三角形相似就出对应线段长度,继而求出点的坐标;
(3)点Q在第一象限角平分线上,设Q(x,x),已知给出了指定角,利用勾股定理列方程,即可求出点Q的坐标;
(4)题目求△ABC为轴对称图形,实质是求动点C,使△ABC为等腰三角形,根据等腰三角形性质分类讨论即可求出点的坐标,利用点的坐标求出运动时间.
解答 解:(1)将点B(0,4)代入直线l的解析式得:
b=4,
∴直线l的解析式为:y=$-\frac{4}{3}$x+4,
令y=0得:x=3,
∴A(3,0).
(2)如图,过点P做直线AB的垂线,垂足为D,
∵OB=4,OA=3,
∴AB=5,
∵∠B是公共角,∠BDP=∠BOD,
∴△BOA∽△BDP,
∴$\frac{OA}{PD}$=$\frac{AB}{BP}$,
∴$\frac{3}{3}$=$\frac{5}{BP}$,
∴BP=5,
4+5=9,4-5=-1,
∴P(0,9)或(0,-1).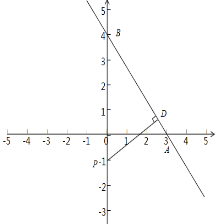
(3)存在.
∵Q在第一象限的角平分线上,
设Q(x,x),
根据勾股定理:
QB2+BD2=QD2,
x2+(x-4)2+52=x2+(x-3)2,
解得x=16,
故Q(16,16).
(4)能使△ABC为轴对称图形,
则得:△ABC为等腰三角形,
当AB=BC时,
C(0,9)或(0,-1),
此时C点运动1秒或11秒,
当AB=AC时,
C(0,-4),
此时C点运动14秒,
当AC=BC时,
C(0,$\frac{7}{8}$),
此时C点运动$\frac{73}{8}$秒.
综上所述:当C点运动1秒、$\frac{73}{8}$秒、11秒、14秒时,能使△ABC为轴对称图形.
点评 题目考查了一次函数的综合应用、点的坐标、相似三角形判定及性质、勾股定理等知识,通过直线的基本性质及三角形的基本性质,找出相应的等量关系即可,题目考查灵活多变,对学生发现问题、解决问题有大的锻炼价值.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
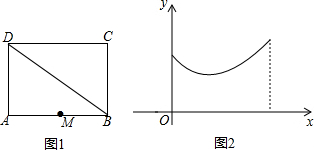 如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )
如图1,正方形ABCD中,点M是AB的中点,点P在某条线段上匀速运动,若运动的时间为x,点P与点M之间的距离为y,且表示y与x的函数关系的图象大致如图2所示,则点P的运动路线可能是( )| A. | A→B | B. | A→D | C. | B→D | D. | D→C |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
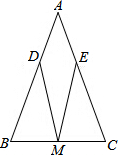 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
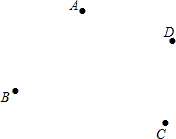 如图,已知四点A、B、C、D,按要求作图
如图,已知四点A、B、C、D,按要求作图查看答案和解析>>
科目:初中数学 来源: 题型:选择题
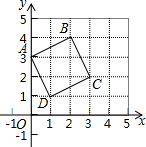 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )| A. | (-1,-4) | B. | (2,4) | C. | (-1,-4) | D. | (1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.
已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com