
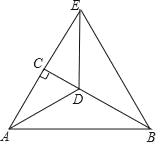
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AD平分∠CAB交BC于点D,CD=1,延长AC到E,使AE=AB,连接DE,BE.
(1)求BD的长;
(2)求证:DA=DE.
【答案】(1)BD=2;(2)证明见解析.
【解析】
(1)根据题意可知∠CAB=60°,想办法证明DA=DB=2CD即可;
(2)由题意可知三角形ABE是等边三角形,然后在证明Rt△DCA≌Rt△DCE,即可求证.
(1)∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,AD平分∠CAB,
∴∠CAB=60°=2×∠CAD,
∴∠CAD=∠DAB=30°;,
∴∠DAB=∠DBA=30°,
∴BD=DA=2CD=2.
(2)∵AE=AB,在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠EAB=60°,
∴△ABE是等边三角形,
∵BC⊥AE,
∴AC=CE,
∵∠ACD=∠DCE=90°,CD=CD,
∴Rt△DCA≌Rt△DCE(SAS),
∴DA=DE.


科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
【尝试】
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
【发现】
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c-10)2=0;
![]()
(1)求a、b、c的值;
(2)动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.若点P到A点距离是到B点距离的2倍,求点P的对应的数;
(3)动点P从A出发向右运动,速度为每秒1个单位长度,同时动点Q从C出发向左运动,速度为每秒2个单位的速度.设移动时间为t秒.求t为何值时,P、Q两点之间的距离为8?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《佛山﹣环西拓规划方案》,三水区域内改造提升的道路约37公里,届时,沿线将串联起狮山、乐平、三水新城、水都基地、白坭等城镇节点,在这项工程中,有一段4000米的路段由甲、乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成的工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用20天.求甲、乙两个工程队平均每天各完成多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
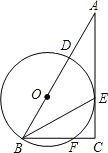
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com